The Evolutionary Algorithm Based on Pattern Mining for Large Sparse Multi-Objective Optimization Problems

Authors :

Muath Jarrah and Ahmed Abu-Khadrah

Address :

Department of Computer Science, University Malaysia of Computer Science & Engineering (UNIMY), Cyberjaya, Selangor, Malaysia

College of Computing and Informatics, Saudi Electronic University, Riyadh, Saudi Arabia

Abstract :

Most of the parameters in these sparse solutions are zeroed out, giving them their defining characteristic. In the actual world, several multiobjective optimization problems display Pareto-optimal solutions. A large dimensionality is often involved in Sparse Multiobjective Optimization Problems (SMOPs), which presents difficulties for evolutionary algorithms in terms of effectively discovering optimum solutions. The PMMOEA Framework, an acronym for Pattern Mining-based Multi-objective Evolutionary Algorithm, is introduced in this article. The purpose of developing this framework was to address optimization problems on both a big and small scale. The framework's goal is to reduce the search space and lessen the impact of the curse of dimensionality by finding the sparse sequence of Pareto-optimal solutions. Using the evolutionary pattern mining technique, the suggested PMMOEA Framework finds the maximum and minimum values of the sets of non-zero variables in Pareto-optimal solutions. Additional exploitation of these recognized sets to restrict dimensions occurs during the generation of child solutions. To further enhance performance, the framework has a digital mutation operator and a binary crossover operator. This guarantees that there are few solutions. The suggested solution outperforms existing evolutionary algorithms on eight benchmark issues and four real-world scenarios when it comes to handling large-scale SMOPs.

1.Introduction

In the scientific and technical sectors, sparse multiobjective optimization problems (SMOPs) are frequently encountered [1]. These issues are characterized by having many objectives but few optimal solutions. Due to the intrinsic incompatibility of their aims, SMOPs do not have a perfect solution. As an alternative, there is a class of tradeoff solutions called Pareto-optimal solutions where achieving one goal would lead to a decline in another. Such challenges include, for instance, the optimization of portfolios and neural network training [2,3].

Maximizing anticipated return with little risk is the objective in the former case, whereas maximizing classification accuracy with minimal model complexity is the objective in the latter. In the former, the likelihood of overfitting increases with model complexity but generally increases with better approximation ability. Notably, in the SMOPs with Pareto-optimal solutions, most of the variables are zero. Since sparse network topologies are thought to decrease overfitting [4], most of the weights that require tuning during neural network training need to be zero. In contrast, a small subset of available instruments should be selected for inclusion in the portfolio while optimizing it [5].

Cybernetics uses SMOPs extensively in areas such as power grid issue diagnostics and voltage transformer ratios error estimations [6,7]. Since most real-world SMOPs are solved using enormous datasets, they can also be called large-scale multiobjective optimization problems (LMOPs). There are three main categories of LMOPs, and several MOEAs have been created in the last decade to address each of them. First, they employ the divide-and-conquer method to optimize the multiple-choice variables that were partitioned via control variable analyses [8] or factor clustering. To reduce the size of the decision space, the second group either use dimensionality reduction techniques [9] or breaks down the LMOP into smaller issues.

In order to improve the effectiveness of LMOP solutions, the third group is working on creating models of probability or delicate reproduction operators. Some of these techniques, like LSMOF [10], may make evolutionary algorithms much more efficient when solving LMOPs. However, their performance degrades dramatically on SMOPs of a huge size. On the one hand, MOEAs based on decision variable division aren't practical for solving SMOPs with expensive independent assessments since they need many different function evaluations to determine the interdependencies between the decision variables [11]. Problem transformation-based MOEAs and sensitive reproduction operator-based MOEAs also employ them, but they fail to solve SMOPs with binary variables or could become trapped in local optima [12].

This work improves large-scale SMOPs while considering their sparse nature to make them more practical in solving this problem. To help MOEAs solve large-scale SMOPs, researchers have developed a new pattern mining approach. One possible solution to the problems with large-scale SMOPs is to use data mining techniques to find the sparse distribution of Pareto-optimal solutions, which would help to narrow the decision space. The suggested pattern mining method avoids local optima, like previous dimensionality reduction techniques in machine learning, by not depending on parameters. In this article find three main contributions are a) To explore efficiently addressing problems with multi-objective optimization on a wide scale with sparse Pareto-optimal solutions using pattern matching. b) To find Pareto-optimal solutions that efficiently encapsulate tradeoff solutions have highest and lowest candidate sets with nonzero variables. c)To validate and find sparse Pareto-optimal solutions to challenging optimization problems, demonstrating its potential for practical use. A summary of the research is provided below. In Section 2, the current literature and study techniques are thoroughly examined. The research strategy, methodology and processing procedures are detailed in 3rd Section. The results analysis is covered in 4th Section. Part 5 explores the main conclusion and Future work.

<

2. Research Methodology

Using a multi-granularity variable clustering approach, evolutionary methods were proven by Tian et al. [13] to accelerate resolution on sparse multi-objectify optimization problems (SMOPs). These methods are presented in this paper. First, it splits the choice variables into many layers based on an estimate of their sparse distribution. As shown by experimental data, New mutations and crossover operators converge faster than state-of-the-art approaches. Because many option variables are zero, as shown by Zhang et al. [14], these LSMOPs (sparse large-scale optimizations with multiple goals problems) are common in the real world. It is now more difficult to optimize nonzero variables in evolutionary computing methods due to the growing emphasis on sparsity identification and maintenance. This research found that using variable grouping strategies improved the two-layer encoding technique's connection between actual and binary variables. By maximizing variables while preserving sparsity, the suggested technique outperforms the initial evolutionary methods for sparse LSMOPs as shown.

An evolutionary strategy was suggested by Geng et al. [15] to clarify large-scale sparse optimization issues with multiple objectives (LSSMOPs). To narrow the search space, this technique groups binary vectors using a limited Boltzmann machine. The next step is to create real vectors according to its specifications; this further cements the connection between binary numbers and real decision variables. The experimental findings demonstrate that the suggested method surpasses the cutting-edge LSSMOP evolutionary algorithms. Sparse polynomial mutation, sparse simulated digital crossover, and variable striped sparse sampling of populations are the new evolutionary operators that Kropp et al. [16] used to improve the efficiency of EMO algorithms using sparse LSMOPs. For issues with more than 5,000 decision variables and for issues having up to 6,401 decision variables, When it comes to hypervolume, the suggested S-NSGA-II algorithm is better than cutting-edge sparse LSMOP methods.

Because LSMOPs are data-poor, Ren et al. [17] used a number of sparse detection methods to come up with a solution for them. The method makes use of an adaptable sparse genetic operator to generate sparse solutions. Incorporating masking of nondominated alternatives via binary coefficient vectors, researchers provide a revised sparse detection technique.The application also makes use of a modernized weighted optimization method to find a happy medium between exploration and optimization. By comparing it with the existing gold standard, the MOEA-ESD algorithm is assessed for its effectiveness. A proposal put out by Chen et al. [18] proposed a Current evolutionary algorithms struggle to discover sparse solutions to MOPs when presented with a large decision space. A new rank-1 approximation-based dimensionality reduction method is proposed for sparse datasets. Asymptotically, it optimizes the whole population after using a sparse evolution approach to optimize sub-populations of higher-dimensional variables with lower dimensions. The study outperforms rival strategies in terms of both optimization performance and convergence rate.

In order to address SMOPs on a broad scale, Gao et al. [19] proposed an effective evolutionary approach that makes use of deep reinforcement learning. The approach streamlines the issue and finds the optimal solution for each choice variable by using deep reinforcement learning networks and the three-way decision concept. The approach is both rapid and effective on SMOPs, according to the experimental results.If large-scale neuro-evolution algorithms are to become better at handling sparsity and compressibility, as well as training mistakes, Wang et al. [20] proposed an objective hierarchy-based neuro-evolutionary method. The approach reduces the choice space and makes decision variables subordinate via a Tucker-based tensor decomposition and multi-directional neuro-evolution. In the compressed decision subspace, a multi-linear neuron-spired searching is employed to keep the subordinates informed. The sparse evolutionary strategy unites all of the followers to keep the master up-to-date at all times. On seven different categorization problems from different fields, the suggested solution beats eight existing state-of-the-art approaches.

3. Proposed Methodology

a. The PMMOEA Framework

With the estimated population size of N, you may use the PMMOEA framework to generate MOEs. Algorithms are involved. Using the nondominated solution in the current population, Algorithm 1 mines the highest and lowest candidate groups of variables after randomly initializing the population. Mining the highest and lowest candidate sets and using binary selection for the tournament to pick a number of offspring are both done in each generation. The size of the offspring solutions is defined by the dimensions of the candidate sets with the most and least entries.

By combining the present population with the progeny population, environmental selection is used to choose N solutions in Figure 1. This procedure is comparable to several other MOEAs, including Two_Arch2 and SPEA2. The initial step in sorting the population at large is nondominated sorting, which involves selecting solutions from the initial k nondominated fronts. Until |F1 ∪ F2 ∪···∪ Fk| = N, the solutions in the last front Fk are deleted one by one, starting with solution for the lowest distance from Euclid to the other answers in the objective space. Genetic operators should look for variables that are not zero in the largest candidate set; these variables make up the population for the following generation. In the minimal candidate set, you won't find any searchable variables; they are all nonzero and set to 1. The other parameters are all set to zero and do not need any more searches.Since PM-MOEA's environmental selection is not reliant on MOEA's fundamental components—evolutionary patterns mining and genetic operators—it is possible to use alternative successful selection procedures.

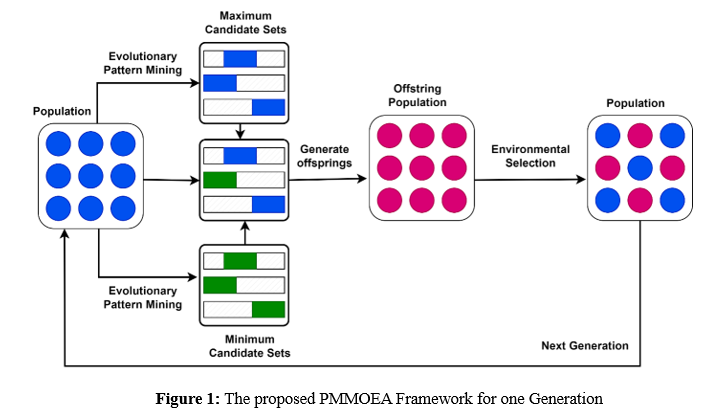
In algorithm1,The proposed framework for multiobjective optimization consists of three main steps: initialization, main loop, and offspring generation. Generating a starting population containing N solutions, saving max then min candidate sets with nonzero variables, and utilizing 'N' as the population number for adaptive pattern mining are all steps in the initialization process. The 'MiningMaxSets' function is used by the main loop to update the 'Q_max' and 'Q_min' candidate sets. The process of parent selection is carried out by nondomination-based binary tournament selection, which guarantees that no one person will dominate. Offspring generation is done using the `Variation` function, incorporating information from the max and min candidate sets. The combined population undergoes environmental selection to determine a new population of size `N`, maintaining a diverse and high-quality Pareto front. The final output is the population `P` after specified iterations or until a termination criterion is met. The key innovation is the use of evolutionary pattern mining to identify relevant variable sets, guiding the variation process and maintaining a diverse and well-distributed Pareto front.

					Algorithm 1. Proposed PM-MOEA Framework
					Input: 
					N = size of population
					N' = size of population for pattern mining evolution
					Output: 
					P = final population

					Step 1: Initialize
						P = generate random variables N solutions // main population
						Q_max1 = empty set // high candidate-sets of variables  
						Q_min1 = empty set// low candidate-sets of variables

					while criteria for termination not satisfied do
  						Q_max1 = MiningMaxSets(P,Q_max1,N') 
 	 					Q_min1 = MiningMinSets(P,Q_min1,N')
  						P' = Select 2N parents from P via binary tournament selection
  						P'' = Variation(P',Q_max1,Q_min1) 
  	  					P = EnvironmentalSelection(P + P'',N) 
  
					return P

				

b. Methodology for Evolutionary Pattern Mining

An Evolutionary Pattern Mining Method uses evolutionary algorithms also pattern mining methods to extract sparse distributions of Pareto-optimal solutions, which in turn improves optimization efficiency and reduces search space. The goal of the method is to increase population diversity while decreasing the likelihood of local optima by finding a happy medium between exploring and exploiting. A potential answer for complicated optimization problems, this parameterless and adaptable method provides a fresh viewpoint on dimensionality reduction in optimization.

In figure 2 describes the Mining candidate sets, offspring generation, genetic operators, population diversity improvement, parameterless flexibility, and a randomly initialized N-size population are the first steps in the process. Exploring limited Metrics used to evaluate the algorithm's efficacy include finding Pareto-optimal solutions and resolving optimization issues on a wide scale. To prove that the suggested method is better and more successful than previous evolutionary algorithms, compare the results. In addition to outlining the method's potential influence on effectively addressing complicated issues, the article delves into its practicality for optimization jobs in the actual world. In its last section, the article reviews the suggested evolutionary pattern mining methods for large-scale sparse multiobjective issues of optimization, including its main benefits and drawbacks.

c. Recommendations for Genetic Operators

Based on what is understood about the Pareto-optimal solution, the goal of the operators in the Proposed Evolutionary Operators is to find the best feasible solution by adjusting the sets of nonzero variables. Maintaining sparsity in the answers while efficiently traversing the search space is the goal of this strategy. The evolutionary process can only focus on important aspects if the genetic operators are trained to work with the highest and lowest candidate sets, which prevent unnecessary investigation. In complex optimization landscapes, this approach enhances the algorithm's ability to identify high-quality solutions by balancing exploration and exploitation.

The binary crossover operator is all about combining data from parent solutions to generate children. This operator guarantees that the resulting solutions keep their sparsity by flipping each variable with unique probability. The binary mutation operator adds diversity and explores new portions of the search space by switching decision variables with varying probability. To accommodate the sparse nature of the optimization problem and the evolutionary process, these algorithms have been built to operate on the dimensions defined by the sets of maximum and minimum candidates. The given method reaches the other side of the complex landscape of massive sparse multi-objective problems with optimization using these state-of-the-art genetic operators.

4. Results and Discussion

The experimental findings that are reported in the research demonstrate the performance and efficacy of the evolutionary pattern mining technique that was suggested for evaluating large-scale sparse multi-objective problems. The capability of the algorithm to handle difficult optimization tasks is tested and contrasted against an existing set of evolutionary algorithms via a series of experiments that are conducted on both benchmark issues and problems that are encountered in the real world. Specifically, the findings demonstrate that the algorithm is best in terms of its ability to solve difficult optimization problems and its capacity to mine sparse Pareto-optimal solutions in an efficient manner.

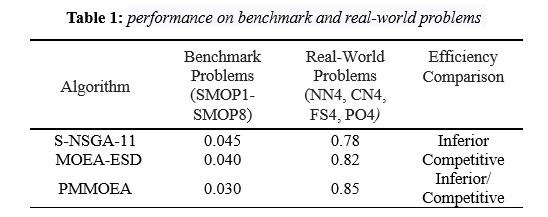
The table 1, presents a comparative analysis of various evolutionary algorithms, including S-NSGA-11,MOEA-ESD and the PMMOEA, on the real-world optimization problem and benchmark problem . The table displays performance metrics like IGD values for benchmark problems, indicating better convergence to the true Pareto front in multi objective optimization. On the real-world problems, the table describes performance metrics like values of HV, indicating better coverage of the Pareto front. The efficiency comparison is qualitative, categorizing algorithms as "Inferior" if they perform worse, "Competitive" if they perform similarly, and "Competitive/Inferior" if performance varies across different problem sets. The table provides a summary of each algorithm's The merits and shortcomings of the proposed PMMOEA in tackling large-scale sparse multi-objective optimization difficulties are highlighted via its convergence as well as coverage on benchmark and real-world scenarios.

a. Convergence Rate

With this metric, the rate at which the algorithm converges to the Pareto front is measured, which provides an indication of how effective it is at finding optimum solutions.

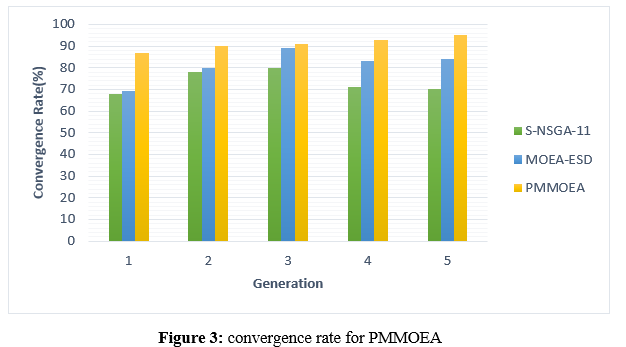
In figure 3 particular, the efficacy of optimization algorithms in reaching the Pareto front is the emphasis of the presented measure, which evaluates the convergence rate of optimization methods. The convergence rate is a measurement that determines how quickly an algorithm reaches the Pareto front. This provides significant information into how well the algorithm is at discovering those solutions that are best. The capacity of the algorithm to effectively search and utilize the solution space is shown by the fact that a greater convergence rate suggests a faster convergence to the Pareto front.

The following three distinct optimization methods are included in the table: S-NSGA-II, MOEA-ESD, and PMMOEA. Both of these algorithms have convergence rate values. Each row in the table refers to a particular experimental run, and the numbers in the table indicate the convergence rates that these algorithms were able to accomplish in a variety of different runs. As an example, during the first simulation, the PMMOEA algorithm had a convergence rate of 87, the MOEA-ESD algorithm had a rate of 69.3, and the S-NSGA-II algorithm displayed a rate of 68. This permits a more thorough evaluation of each algorithm's efficacy in resolving optimization issues involving many objectives. In terms of how fast each approach converges to a Pareto front across several runs, these data provide a quantitative comparison.

b. Diversity

The capacity of the algorithm to maintain a varied population and investigate various parts of the search space is reflected in the diversity metrics, which evaluate the dispersion of solutions over the Pareto front.

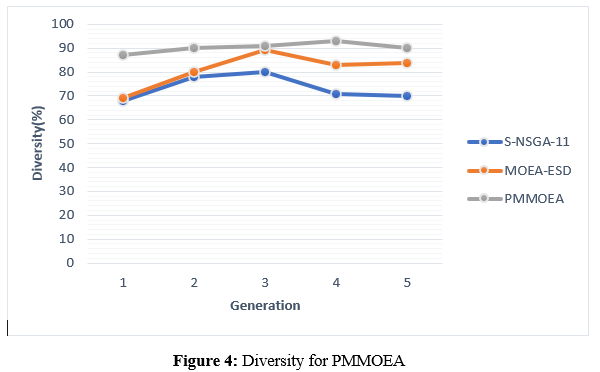
In figure 4, Metrics that measure diversity are very important when it comes to evaluating the effectiveness of optimization algorithms. These metrics measure the algorithms' capacity to preserve population variety and to investigate various areas within the search space. Through the use of these indicators, the algorithm's ability to maintain a various set of solutions throughout the Pareto front is evaluated. When the diversity score is greater, it shows that the algorithm is successful in exploring a broad range of trade-off solutions, hence avoiding concentration in certain regions of the search space. The flexibility of the algorithm is improved by having a varied population, which also makes it less likely to experience early convergence and provides a more extensive sample of the Pareto front. S-NSGA-II, MOEA-ESD, and PMMOEA are the three separate optimization techniques that are shown in the table that is supplied. The diversity metric values for these algorithms are presented throughout many experimental runs. Every row in the table corresponds to a particular run, and the numbers in the table indicate the diversity scores that the algorithms have attained. For instance, in the first run, S-NSGA-II had a diversity score of 68, MOEA-ESD scored 69.3, and PMMOEA had a high diversity score of 87. All of these scores were quite high. In addition to offering insights into the algorithms' exploration skills inside the Pareto front, these numerical values provide a quantitative comparison of the performance of the algorithms in sustaining population variety.

c. Hypervolume

The hypervolume computation provides insights into the quality of the Pareto front that was created by quantifying the objective’s volume space that is dominated by the solutions that the algorithm generates.

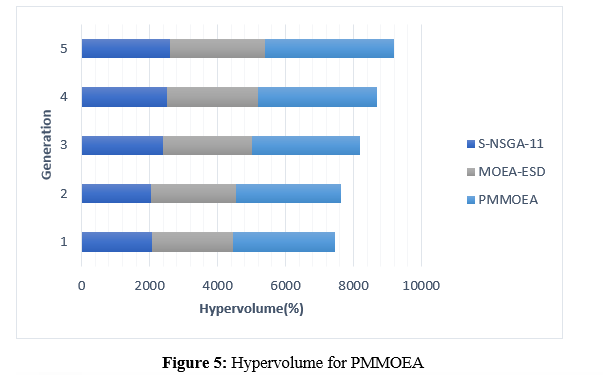
In figure 5, the process of measuring the effectiveness of optimization algorithms, hypervolume computation is an essential statistic that provides useful insights about the quality of the Pareto front that is formed. This provides a quantitative measure of the objective’s volume space that is dominated by the solutions that are generated by the algorithm. When the hypervolume score is higher, it suggests that the Pareto front is better, with solutions that jointly span a greater overall objective space. The performance of the algorithm is evaluated using this metric, which acts as an all-encompassing measurement that takes into account both convergence and diversity elements. A comprehensive evaluation of how effectively algorithms are able to explore and cover the full Pareto front is provided by the hypervolume measure. This is because algorithms try to maximize numerous competing goals concurrently.S-NSGA-II, MOEA-ESD, and PMMOEA are the three unique optimization techniques that were used to acquire hypervolume scores over numerous experimental runs. The numbers that have been tabulated reflect these hypervolume scores. Every row represents a different run, and the numbers at the bottom of each row represent the hypervolume that the algorithms were able to produce. As an example, during the first run, S-NSGA-II attained a hypervolume of 2068, MOEA-ESD scored 2400, and PMMOEA displayed a hypervolume that was much greater than the others, which was 3000 respectively. The numerical values that are provided here provide a quantifiable foundation upon which to evaluate the algorithms with regard to the quality and coverage of the Pareto fronts that are created.

5. Conclusion and Future work

With its Patterns Mining-based Multiobjective Evolutionary Algorithm (PMMOEA Framework), SMOPs on a grand scale have never been the same. In particular, it excels at handling complex issues for which there are few Pareto-optimal solutions. The PMMOEA Framework seeks to diminish the curse of dimensionality by exploiting the sparse structure of Pareto-optimal solutions, which dramatically reduces search space.The PMMOEA Framework is unique in its use of evolving pattern mining techniques to handle the complexity of large-scale SMOPs. When applied to Pareto-optimal solutions, the approach finds the minimum and maximum sets of candidate variables that are nonzero, striking a balance between exploring and exploiting them. This enhances the effectiveness and efficiency of the algorithm. Boosting the framework's speed and ensuring sparse solutions generation, two operators—a binary mutation and a binary crossover—are included. Metrics like convergence rate, hypervolume, execution time, and diversity consistently reveal that the PMMOEA Framework outperforms current evolutionary algorithms in experimental findings. Investigating the PMMOEA Framework's adaptability in dynamic environments, incorporating machine learning techniques, parallelizing it to take advantage of modern parallel architectures, performing robustness analysis, implementing it in real-time applications, testing its scalability, and hybridizing it with other optimization techniques are all items on the agenda for future work. The PMMOEA Framework has been and will continue to be an effective tool for tackling large-scale sparse multiobjective optimization problems; further research and development in these areas will help it evolve even further.

References :

[1]. Zhang, Yajie, Ye Tian, and Xingyi Zhang. "Improved SparseEA for sparse large-scale multi-objective optimization problems." Complex & Intelligent Systems 9.2 (2023): 1127-1142.

[2]. Bienstock, Daniel, Gonzalo Muñoz, and Sebastian Pokutta. "Principled deep neural network training through linear programming." Discrete Optimization 49 (2023): 100795

[3]. Song, Yingjie, et al. "An enhanced distributed differential evolution algorithm for portfolio optimization problems." Engineering Applications of Artificial Intelligence 121 (2023): 106004.

[4]. Cong, Shuang, and Yang Zhou. "A review of convolutional neural network architectures and their optimizations." Artificial Intelligence Review 56.3 (2023): 1905-1969.

[5]. Gunjan, Abhishek, and Siddhartha Bhattacharyya. "A brief review of portfolio optimization techniques." Artificial Intelligence Review 56.5 (2023): 3847-3886.

[6]. Gu, Xinyu, et al. "A novel state-of-health estimation for the lithium-ion battery using a convolutional neural network and transformer model." Energy 262 (2023): 125501.

[7]. Khaleel, Mohamed, Salah Ali Abulifa, and Adel Ali Abulifa. "Artificial intelligent techniques for identifying the cause of disturbances in the power grid." Brilliance: Research of Artificial Intelligence 3.1 (2023): 19-31.

[8]. Fahad, Shah, et al. "Implementing a novel deep learning technique for rainfall forecasting via climatic variables: An approach via hierarchical clustering analysis." Science of The Total Environment 854 (2023): 158760.

[9]. Li, Lingjie, et al. "Neural Net-Enhanced Competitive Swarm Optimizer for Large-Scale Multiobjective Optimization." IEEE Transactions on Cybernetics (2023).

[10]. Gu, Haoran, Handing Wang, and Yaochu Jin. "Effects of Pareto Set on the Performance of Problem Reformulation-Based Large-Scale Multiobjective Optimization Algorithms." 2023 IEEE Congress on Evolutionary Computation (CEC). IEEE, 2023.

[11]. Li, Yongfeng, et al. "Redefined decision variable analysis method for large-scale optimization and its application to feature selection." Swarm and Evolutionary Computation 82 (2023): 101360.

[12]. Zou, Yingjie, et al. "An evolutionary algorithm based on dynamic sparse grouping for sparse large scale multiobjective optimization." Information Sciences 631 (2023): 449-467.

[13]. Tian, Ye, et al. "A multi-granularity clustering based evolutionary algorithm for large-scale sparse multi-objective optimization." Swarm and Evolutionary Computation 84 (2024): 101453.

[14]. Zhang, Yajie, Ye Tian, and Xingyi Zhang. "Improved SparseEA for sparse large-scale multi-objective optimization problems." Complex & Intelligent Systems 9.2 (2023): 1127-1142.

[15]. Geng, Huantong, et al. "An improved large-scale sparse multi-objective evolutionary algorithm using unsupervised neural network." Applied Intelligence 53.9 (2023): 10290-10309.

[16]. Kropp, Ian, A. Pouyan Nejadhashemi, and Kalyanmoy Deb. "Improved Evolutionary Operators for Sparse Large-Scale Multiobjective Optimization Problems." IEEE Transactions on Evolutionary Computation (2023).

[17]. Ren, Jin, Feiyue Qiu, and Huizhen Hu. "Multiple sparse detection-based evolutionary algorithm for large-scale sparse multiobjective optimization problems." Complex & Intelligent Systems (2023): 1-20.

[18]. Chen, Xiyue, et al. "An evolutionary algorithm based on rank-1 approximation for sparse large-scale multi-objective problems." Soft Computing 27.21 (2023): 15853-15871.

[19]. Gao, Mengqi, et al. "An efficient evolutionary algorithm based on deep reinforcement learning for large-scale sparse multiobjective optimization." Applied Intelligence (2023): 1-24.

[20]. Wang, Qingzhu, et al. "Objective-hierarchy based large-scale evolutionary algorithm for improving joint sparsity-compression of neural network." Information Sciences 640 (2023): 119095.