Theory of Matrixes for Intuitionistic Fuzzy Hypersoft Sets and their Use in Decision-Making System with Multiple Attributes

Authors :

Mary Jansi Rani and Periyasamy

Address :

SRM Institute of Science and Technology, Trichy

Department of Computer Science, periyar University, Salem

Abstract :

Through the integration of matrix theory with sets of intuitionistic fuzzy hypersoft variables, the Matrix-based Intuitionistic Fuzzy Hypersoft Decision Framework (MIFHDF) is presented in this research. The MIFHDF is designed to improve decision-making systems that face many qualities. As a result of the incorporation of innovative ideas and approaches, the framework provides a comprehensive solution for the management of unclear decision-making processes. MIFHDF is a sophisticated approach that leverages matrix operations to analyze and evaluate complex decision scenarios. subsequently does this by extending standard intuitionistic fuzzy sets from hypersoft sets and fuzzy sets. In order to put an emphasis on the practical usability and effectiveness of matrix-based methodologies in addressing real-world decision issues, the theoretical foundation of the framework has been rigorously constructed. Based on the employment of intuitionistic fuzzy hypersoft sets and matrix theory, MIFHDF offers decision-makers a strategy that is both structured and systematic, allowing them to navigate complex choice landscapes that contain numerous qualities. The one-of-a-kind insights and analytical methodologies that are presented in this study pave the way for future advancements in the field of decision-making systems, particularly in circumstances that are characterized by ambiguity and a wide variety of criteria.

1.Introduction

In the world of decision-making systems, the capacity to successfully navigate through complicated scenarios that are marked by ambiguity, vagueness, and various qualities is fundamental to the achievement of optimal results [1]. Matrix theory integrated with intuitionistic fuzzy hypersoft sets gives a viable route for improving decision-making processes in situations that are as difficult as the ones we are currently experiencing [2]. Within the scope of this study, the Matrix-based Intuitionistic Fuzzy Hypersoft Decision Framework (MIFHDF) is presented as an all-encompassing solution that is intended to tackle the complexities of decision-making systems that require numerous qualities [3]. Utilizing the power of matrix operations, the MIFHDF framework is a sophisticated approach that is utilized for the purpose of analyzing and evaluating difficult decision scenarios [4]. Through the incorporation of fresh ideas and approaches, as well as the extension of standard intuitionistic fuzzy sets to hypersoft sets, MIFHDF provides decision-makers with an organized and systematic strategy that enables them to effectively traverse through choice landscapes that contain a variety of qualities [5]. In order to offer decision-makers with a tool that is both practical and effective in managing ambiguity and vagueness, the framework's ultimate goal is to provide decisions that are both informed and optimal. Subsequently has been methodically created to stress the MIFHDF framework's practical usefulness and efficacy in handling real-world decision difficulties [6].

The theoretical underpinning of the framework has been constructed [7]. Through the utilization of the ideas of intuitionistic fuzzy hypersoft sets and matrix theory, MIFHDF provides decision-makers with a robust methodology that boosts their capacity to make informed decisions in situations that are both complicated and uncertain [8]. This research presents a number of novel insights and analytical approaches that have the potential to pave the way for future breakthroughs in decision-making systems, particularly in situations that are characterized by ambiguity and a large diversity of criteria [9]. The purpose of this introduction is to lay the groundwork for the subsequent in-depth examination of the MIFHDF architecture and its use in decision-making systems that contain many attributes [10]. Providing a comprehensive understanding of how such innovative approaches can revolutionize decision-making processes in complex and uncertain environments is the goal of this research [11]. This will be accomplished by delving into the theoretical underpinnings and practical implications of integrating matrix theory with intuitionistic fuzzy hypersoft sets [12]. The main objectives of the MIFHDF are:

• To develop a comprehensive understanding of the Matrix-based Intuitionistic Fuzzy Hypersoft Decision Framework (MIFHDF) and its integration of matrix theory with intuitionistic fuzzy hypersoft sets.
• Investigate the way MIFHDF can enhance decision-making systems facing challenges related to ambiguity, vagueness, and multiple attributes.
• Explore the innovative ideas and approaches incorporated in MIFHDF to provide a structured and systematic strategy for decision-makers.
• Evaluate the practical usability and effectiveness of matrix-based methodologies in addressing real-world decision issues within the context of MIFHDF.
• Examine the extension of standard sets of intuitionistic fuzzy hypersoft variables and fuzzy set within the framework of MIFHDF.

A summary of the research is provided below. In Section 2, the current literature and study techniques are thoroughly examined. The research strategy, methodology and processing procedures are detailed in 3rd Section. The results analysis is covered in Section 4. Part 5 explores the main conclusion and Future work.

2.Research Methodology

Some researchers, including Jafar et al. [13], In this case, the environment is not precise, not clear, and not predictable; this makes decision-making more difficult, especially when there are several and further split attributes. Smaranndache proposed a neutrosophics hypersoft set as a solution to such problems. This study extends the previous work on neutrosophics hypersoft sets (NHSs) to investigate neutrosophics hypersoft matrix (NHSMs) with suitable examples. A few standard approaches for NHSM have been produced through research that utilizes analysis. Lastly, a new approach to selecting college professors has been proposed, based on a score function, and the numerical analysis of its decision-making concerns has been completed. This study refines the NHSM algorithm for optimal choice selection in a way that is both efficient and easy to use, with the goal of solving decision-making problems.

Hypersoft sets (HSS) have been proposed by Smarandache to provide decision-makers with additional possibilities. HSS replaces the single parameter function found in soft sets (SS) with a multi-attribute function, as demonstrated by Debnath et al. [14]. It is a hybrid structure that combines hypersoft sets with interval-value intuitionistic fuzzy set (IVIFS). Important decision-making operations on interval-value intuitionistic fuzzy hypersoft set (IVIFHSSs) are introduced and examined in this paper. By mixing operators like complement, union, intersection, either OR, AND, etc., IVIFHSSs are able to handle real-world problems with partial or parameterized knowledge. A newly-initiated procedure based on IVIFHSSs is shown to be valid and reliable using a numerical example. Some of the expected uses of the concept include data clustering, medical diagnostics, personality selection, weather forecasting, and parameter reduction.

Hypersoft, as described by Ur Rahman et al. [15], is an extension of soft set that divides every characteristic into its own collection of value-atributed attributes. This structure's increased utility and adaptability are results of its solution to the soft set problem of continuous attribute-valued collections for individual attributes. Neutrophil parametric soft set literature is to be brought into harmony with multi-attribute approximation function in this work. Also, before we go into the set theoretic operations and important aspects of neutrosophic parameterized hypersoft sets, we need define these sets as fuzzy, intuitionistic, or neutrosophic sets. Next, develop algorithms for making decisions based on these speculations. Examples also show that the approach is structurally valid, which is crucial for solving issues involving ambiguity and uncertainty. We conclude by investigating the structure's applicability.

According to Ihsan et al. [16], parameters are crucial in every decision-making situation; nevertheless, experts need to sort out ambiguous parameters by giving them a fuzzy membership grade. There is currently no model available from the field of fuzzy parameterization that can deal with hypersoft environments, expert preferences, or intuitionistic settings. We decided to look into this vulnerability because of it. To overcome the limitations of previous models, such as FPIFSES, for multi-argument approximate functions, this study describes the fuzzy parameterized intuitionistics fuzzy hypersoft experts sets (FPIFHsES). Using this technique, FPIFHsES can deal with real-world cases when discontinuous sets of sub-attribute values are required for attribute classification. The FPIFHsES gains greater adaptability and reliability through the use of deep attribute analysis within the decision-support system. In FPIFHsES, we find theoretical, axiomatic, and algorithmic approaches.

Hypersoft sets are a new field of study that, according to Rahman et al. [17], deal with practical problems that call for sub-parametric value classifications as overlapping sets of parameters. As its domain, a new approximate mapping is applied to sub-parametric tuples. Structures similar to existing soft sets are unmanageable. By utilizing unknown parts of intuitionistic and neutrosophic sets, this study seeks to generate a novel approach to parameterizing fuzzy sets in hypersoft environments. With the help of algebraic tools like theory, examination, representation, and algorithms, two novel structures, are built. By examining the fundamental characteristics and set-theoretic operations of fpifhss’-set and fpnhs’-set, two distinct algorithms are provided to deal with the actual COVID-19 decision-making issue. In order to assess the merits of these algorithms, their results are contrasted with well-established models.

A powerful tool for incorporating insecure information into decision-making, the intuitionistic fuzzy hypersoft set (IFHSS) was extended to interval-valued IFHSS (IVIFHSS) by Zulqarnain et al. [18]. This research presents a variety of aggregation operators (AOs), including IVIFHSWA and IVIFHSWG, which stand for interval-valued fuzzy intuitionistic and hypersoft weighted geometric operators. The goal of the study is to suggest IVIFHSS algebraic operational rules. The proposed MCGDMs process for material selections in cryogenic storage vessels overcomes the contradictory results of existing approaches and is presented for practical use. To address these concerns, the MCGDMs approach was created. The constructed model is more effective and consistent for managing IVIFHSS-based information.

The goal of Hema et al. [19] was to analyze a plithogenic intervals valued neutrosophic hypersoft set in order to improve the accuracy of environments when several criteria are considered. A hybrid of hypersoft neutrosophic and plithogenic fuzzy sets, this set possesses all three properties. By comparing the results to Fuzzy-TOPSIS in two distinct settings with varying weightages, the suggested TOPSIS algorithm—which comprises tnorms, tconorms, an accuracy ratio, and a plithogenics interval valued hypersoft sets—has been validated. More precision for linguistic variables, as opposed to sharp values, is possible with the new idea. An example of a multi-criterion decision-making environment is solved using the proposed method.

A more sophisticated version of the intuitive fuzzy hypersoft set (IFHSS), the Pythagorean fuzzy hypersoft set (PFHSS) was introduced by Siddique et al. [20] and is used to evaluate DM insufficiencies, anxiety, and reluctance. Among existing methods, it accommodates most uncertainty and is hence the most substantial concept for DM operations involving fuzzy dataPythagorean fuzzy hypersoft average Weighted Average (PFHSWA) and ambiguous hypersoft weighted geometrical (PFHSWG) operators are introduced and explained in this work, along with their essential qualities such as boundedness, idempotency, shift-invariances, and homogeneous. Presented the aggregation operators (AOs) underpin a new MCDM approach. To prove the method's viability, a contrast study was done.

3.Proposed Methodology

a. Conceptual Framework Development

The main objective of this step is to define key concepts and establish the theoretical framework for integrating matrix theory with intuitionistic fuzzy hypersoft sets to form MIFHDF. Matrix Theory: In matrix theory, a matrix is represented as A=[aij] (1) Elements of the matrix are represented by the letters aij in equation 1. Sets of Intuitionistic Fuzzy Hypersoft Variables: the representation of an intuitionistisc fuzzy hypersoft sets is as follows: A={(x,μA(x),νA(x))} (2) In the equation 2, the variable x is a member of the sets. The membership functions, denoted as μA(x), is a function that indicates the extent to which x is a member of the set. The non-membership function, denoted as vA(x), is a function that indicates the extent to which x does not exist within the set.

.In figure 1, The flowchart depicts the step-by-step process of defining important concepts and establishing the theoretical framework for merging matrix theory with intuitionistic fuzzy hypersoft sets to generate MIFHDF. - The flowchart also shows how the process is carried out. With the purpose of facilitating comprehension of the development of the conceptual framework, it provides a graphical representation of the flow of information and concepts in a structured manner. The process starts with the identification of the necessity to integrate matrix theory with sets of intuitionistic fuzzy hypersoft variables. This is the first step in the process. Definition of Matrix Theory: Define the fundamental concepts of matrix theory, including the elements that are represented by the symbol A=[aij]. Definition of Intuitionistic FuzzyHypersoft Sets: Define the components of an intuitionistic fuzzy hypersoft set, including elements, the membership functions μA(x), and the non-membership functions νA(x).Integration: Demonstrate how matrix theory can be integrated with intuitionistic fuzzy hypersoft sets in order to create MIFHDF.A theoretical framework that integrates matrix theory with intuitionistic fuzzy hypersoft sets should be developed as part of step five, which is the establishment of the theoretical framework. After the completion of the process, the conceptual framework for MIFHDF is established. This marks the end of the procedure. In order to accomplish the creation of the MIFHDF framework, this flowchart provides a visual representation of the logical sequence that involves establishing essential ideas and merging matrix theory with intuitionistic fuzzy hypersoft sets. It acts as a guide for researchers to comprehend the fundamental components of the approach that is being proposed that is being proposed.

b. Extension of Sets of Intuitionistic Fuzzy Hypersoft Variables

Extend intuitionistic fuzzy sets to hypersoft and fuzzy sets within MIFHDF to handle complexities of decision scenarios with multiple attributes. Extension of Intuitionistic Fuzzy Sets to Hypersoft Sets: A={(x,μA(x),νA(x),λA(x))} (3) In equation 3, λA(x) represents the neutral function. The set contains x as one of its elements. An example of a membership function is denoted by the symbol μA(x), which represents the extent to which x is a member of the set. Indicating the extent to which x does not belong to the set, the non-membership function is denoted by the expression vA(x). The neutral function, denoted by λA(x), is a function that represents the degree of neutrality or hesitancy with respect to the representation of x inside the set.

Definition 2 states that a set of traversal of 𝑘’ exclusive vertices in a graph 𝐺′ (𝑡𝑟 ⊆ 𝑉 (𝐺′)) that stores the order in which each vertex 𝑣 ∈ 𝑡𝑟 is visited in 𝐺′. Existing edges among the vertices accompany an induced traversal.

Definition 3: A bijective function 𝑓 ∶ 𝑉 (𝐺′) → 𝑉 (𝐻) is an isomorphism between two graphs G’ and 𝐻 if and only if, for every edge (𝑣𝑖, 𝑣𝑗) ∈ 𝐸(𝐺′), (𝑓(𝑣𝑖), 𝑓(𝑣𝑗)) ∈ 𝐸(𝐻).

Automorphisms are graphs 𝐺 ′and 𝐻 that are isomorphic to each other, defined as 𝑉 (𝐺′) = 𝑉 (𝐻).

If a graph G' and a set of traversals T create the same inspired traversal trind, the definitive option is the single T traversal that can reach G' trind with the allowed visited order of vertices.By limiting themselves to canonical possibilities, GPM algorithms eliminate wasteful computation by ensuring that no two exploration traversals end up at the same induced traversal. It is possible to transform canonical candidates into a distinct representation known as a canonical representative, or pattern, in this context. Canonical labeling is a common procedure in GPM methods for subgraph classification; it involves converting an induced traversal to its canonical representation.

3. Proposed Methods for Mining GPU Graphics Patterns Efficiently

Graph pattern mining techniques that make good use of graphics processing units (GPUs) are detailed here. In this first section, the study provides a brief introduction to GraphDuMato, our technology that enables the GPU application of GPM algorithms at a great level. After that, the study shows that the way plan is to lessen memory request, boost memory combination and separations, and lessen load imbalance using the GraphGraphDuMato execution process.

In figure 2, The fuzzy flowchart is a visual representation of the method of extending sets of intuitionistic fuzzy variables to hypersoft sets within MIFHDF in order to manage decision situations that involve numerous characteristics. The method starts with the goal of expanding intuitionistic fuzzy sets to hypersoft sets within MIFHDF. This is the first step in the method. Intuitionistic fuzzy sets define the following: the elements, membership functions, and non-membership functions that are included in intuitionistic fuzzy sets. Hypersoft Sets are extended to include: Introducing the idea of hypersoft sets can be accomplished by incorporating the neutral function λ A (x) into the existing representation of sets of intuitionistic fuzzy variables.

The inclusion of the neutral functions makes it possible to handle complications in choice scenarios that involve numerous qualities. This is accomplished by capturing the degree of neutrality or reluctance being displayed by the individual. There is integration with MIFHDF: In the context of the more general framework of MIFHDF, demonstrate how the expansion of intuitionistic fuzzy sets to hypersoft sets fits in context. The procedure comes to a successful conclusion with the successful extension of intuitionistic fuzzy sets to hypersoft sets, which enhances the capabilities of decision-making inside MIFHDF. The process of this flowchart is to provide an organized overview of the extension process. It does so by highlighting the major components and the rationale behind the extension of sets of intuitionistic fuzzy variables to hypersoft sets within the context of MIFHDF. Researchers that are interested in improving decision-making methods in complex scenarios might use it as a visual guide to help them achieve their goals.

c. Matrix Operations Analysis

The purpose of the Matrix Operations Analysis, which is being conducted within the framework of the Theory for Neutrosophic Hypersoft Set Matrix(NHSM) and the Multi attributive Multi criteria Decision-Making Framework (MIFHDF), is to investigate and investigate the application of matrix operations in the process of effectively evaluating complex decision scenarios. The objective is to improve the decision-making process by offering a structured and quantitative approach to dealing with uncertainties and complexities. This will be accomplished by utilizing matrix operations such as addition, multiplication, inversion, and other operations. Matrix Operations: The analysis includes a number of different matrix operations, each of which plays an important part in the cases where decisions are being made. Many of the most important matrix operations are as follows: Mixing matrices in order to produce a sum matrix is an example of addition. Carrying out matrix multiplication in order to obtain a product matrix is an example of multiplication. Finding the inverse of a matrix in order to solve equations and find answers is what is meant by the phrase inversion. Changing the rows and columns of a matrix in order to make calculations easier is referred to as transposition. The calculation of a matrix's determinant in order to evaluate its attributes is referred to as determinant calculation. In order to gain an understanding of the features of a matrix, eigenvalue and eigenvector analysis involves determining eigenvalues and eigenvectors.

In figure 3, A visual representation of the process of analyzing matrix operations within the MIFHDF framework for the purpose of properly evaluating complicated decision situations is provided by the Matrix Operations Analysis Flowchart. Programming begins with the purpose of investigating matrix operations for the purpose of decision-making. These operations include matrix addition, matrix multiplication, matrix inversion, transposition, determinant computation, eigenvalue and eigenvector analysis, and conclusion. A structured overview of the matrix operations analysis process is provided by the flowchart. The presentation highlights significant operations and the significance of those operations in improving decision-making procedures within the MIFHDF framework. It acts as a visual reference for scholars and practitioners who are interested in utilizing matrix operations for the purpose of analyzing complicated decision situations in a manner that is both precise and efficient. Those scholars and practitioners who are interested in utilizing matrix operations for decision-making will find the flowchart to be an extremely helpful tool.

4. Result and discussion

The experimental setup aims to validate the effectiveness and efficiency of the Theory for Neutrosophic Hypersoft Set Matrix (NHSM) in Multi attributive Multi criteria Decision-Making (MCDM) problems. A dataset with multiple attributes and decision-makers is used to simulate real-world decision scenarios. The NHSM algorithm, incorporating matrix operations and score functions, is implemented to evaluate and rank objects based on decision criteria.Results from the experiment include data preprocessing, matrix operations application, score calculation, ranking and comparison, performance evaluation, visualization, and discussion and interpretation. Data is preprocessed to convert neutrosophic values into NHSM matrices representing attributes and decision-makers' preferences. Matrix operations such as addition, multiplication, and inversion are applied to manipulate NHSM matrices and derive intermediate matrices for score calculation.Scores for each object are calculated using NHSM matrices and intermediate matrices obtained from matrix operations. Higher scores indicate better suitability for selection. The ranking results are compared with existing decision-making techniques to evaluate the algorithm's performance.

Performance evaluation measures accuracy, efficiency, and scalability. Visual aids enhance the interpretation of results and provide insights into the effectiveness of the NHSM algorithm.The results are discussed in detail, highlighting the algorithm's performance in solving complex decision-making problems and its potential for improving decision outcomes. The comparative analysis with existing techniques validates the algorithm's performance and showcases its potential for advancing decision-making methodologies in uncertain and vague environments.

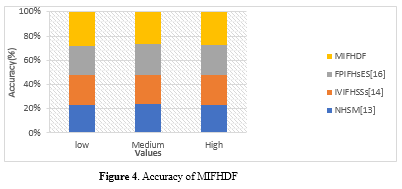
In figure 4, The degree to which the rankings generated by the MIFHDF algorithm correspond to the results which are anticipated in decision-making scenarios is referred to as the algorithm's accuracy. In essence, it evaluates the degree of accuracy or precision that the algorithm possesses in terms of its forecasts or ranks or rankings. An accuracy that is higher implies that the rankings produced by the algorithm closely match the outcomes that were anticipated or wanted, whereas an accuracy that is lower suggests that there are inconsistencies or flaws in the rankings. In conclusion, accuracy is a form of evaluation that determines how effective MIFHDF is in creating rankings that are in accordance with the outcomes that are anticipated from decision-making procedures.

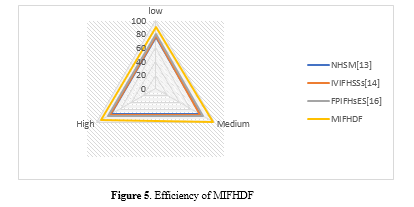
In figure 5,The MIFHDF algorithm's efficiency may be measured by analyzing the amount of time it takes to generate results as well as the amount of computational complexity it possesses. The term "efficiency" refers to the degree to which an algorithm is able to effectively utilize computational resources in order to create results. When compared to algorithms that are less efficient, a MIFHDF algorithm that is extremely efficient calls for a shorter amount of computational time and resources to generate results. When it comes to practical applications, where fast decision-making is critical, evaluating efficiency is essential since it helps determine the performance of the algorithm in terms of speed and resource consumption.

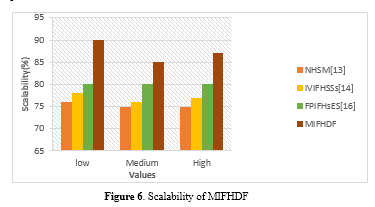
In figure 6,The efficiency with which MIFHDF handles datasets that grow in size or complexity is what we mean when we talk about their scalability. Basically, it checks if the algorithm can process more complicated or bigger datasets without drastically lowering its performance. It is expected that a scalable MIFHDF algorithm can keep performing well even when presented with increasingly complex decision-making situations or bigger data sets. For the approach to be applicable and dependable in real-world applications, where the quantity and complexity of datasets can fluctuate, scalability is essential.

5. Conclusion and Future work

The Matrix Theory for Neutrosophic Hypersoft Set (NHSM) represents a significant improvement in decision-making approaches, notably in the content of Multi attributive Multi criteria Decision-Making (MCDM) situations. Matrix theory and set of intuitionistic fuzzy hypersoft variables are both incorporated into the MIFHDF framework, which provides a solid basis for dealing with complex decision scenarios that involve numerous characteristics. In the process of addressing MCDM situations that include a high number of decision-makers, the suggested algorithm, which is based on NHSM, proves both its practicability and its efficiency. For the purpose of demonstrating the reliability and validity of the suggested methodology, comparison analysis with existing approaches is utilized. This study also highlights the correctness and application of the proposed strategy in real-world decision scenarios. It is possible to further improve the accuracy and reference value of the algorithm by taking into account the interrelationships between attributes and by having the capability to accommodate correlations. Enhanced algorithm development, real-world applications, dynamic decision environments, machine learning integration, validation and benchmarking, and user-friendly interfaces should be the primary focuses of research in the future. Taking into consideration these potential future research topics will allow the field of decision-making to reap the benefits of the ongoing development and improvement of the NHSM framework. This will ultimately result in decision-making processes that are more effective and efficient in situations that are both complex and uncertain.

References :

[1]. Muhsen, Yousif Raad, et al. "Evaluation of the routing algorithms for NoC-based MPSoC: a fuzzy multi-criteria decision-making approach." IEEE Access (2023).

[2]. Aungkulanon, Pasura, et al. "Fuzzy Techniques and Adjusted Mixture Design-Based Scenario Analysis in the CLMV (Cambodia, Lao PDR, Myanmar and Vietnam) Subregion for Multi-Criteria Decision Making in the Apparel Industry." Mathematics 11.23 (2023): 4743.

[3]. Alsalem, M. A., et al. "Multi-criteria decision-making for coronavirus disease 2019 applications: a theoretical analysis review." Artificial Intelligence Review 55.6 (2022): 4979-5062.

[4]. Gamal, Abduallah, et al. "An Interactive Multi-Criteria Decision-Making Approach for Autonomous Vehicles and Distributed Resources Based on Logistic Systems: Challenges for a Sustainable Future." Sustainability 15.17 (2023): 12844.

[5]. Rath, Constanze Ruesga, Sina Grosskopf, and Christoph Barmeyer. "Leadership in the VUCA world-a systematic literature review and its link to intercultural competencies." European Journal of Cross-Cultural Competence and Management 5.3 (2021): 195-219.

[6]. Zeng, Fanlong, et al. "Large language models for robotics: A survey." arXiv preprint arXiv:2311.07226 (2023).

[7]. Moslem, Sarbast. "A novel parsimonious spherical fuzzy analytic hierarchy process for sustainable urban transport solutions." Engineering Applications of Artificial Intelligence 128 (2024): 107447.

[8]. Lotfi, Farhad Hosseinzadeh, et al. Fuzzy Decision Analysis: Multi Attribute Decision Making Approach. Vol. 1121. Springer Nature, 2023.

[9]. Zulqarnain, Rana Muhammad, et al. "Robust aggregation operators for intuitionistic fuzzy hypersoft set with their application to solve MCDM problem." Entropy 23.6 (2021): 688.

[10]. Rahman, Atiqe Ur, et al. "Decision making algorithmic techniques based on aggregation operations and similarity measures of possibility intuitionistic fuzzy hypersoft sets." AIMS Math 7.3 (2022): 3866-3895.

[11]. Zulqarnain, Rana Muhammad, et al. "Aggregation operators for interval-valued intuitionistic fuzzy hypersoft set with their application in material selection." Mathematical Problems in Engineering 2022 (2022).

[12]. Yolcu, Adem, Florentin Smarandache, and Taha Yasin ÖZTÜRK. "Intuitionistic fuzzy hypersoft sets." Communications faculty of sciences University of Ankara Series A1 mathematics and Statistics 70.1 (2021): 443-455.

[13]. Jafar, Muhammad Naveed, and Muhammad Saeed. "Matrix theory for neutrosophic hypersoft set and applications in multiattributive multicriteria decision-making problems." Journal of Mathematics 2022 (2022): 1-15.

[14]. Debnath, Somen. "Interval-valued intuitionistic hypersoft sets and their algorithmic approach in multi-criteria decision making." Neutrosophic Sets Syst 48 (2022): 226-250

[15]. Ur Rahman, Atiqe, et al. "Decision making algorithmic approaches based on parameterization of neutrosophic set under hypersoft set environment with fuzzy, intuitionistic fuzzy and neutrosophic settings." Computer Modeling in Engineering & Sciences 128.2 (2021): 743-777.

[16]. Ihsan, Muhammad, et al. "An intelligent fuzzy parameterized multi-criteria decision-support system based on intuitionistic fuzzy hypersoft expert set for automobile evaluation." Advances in Mechanical Engineering 14.7 (2022): 16878132221110005.

[17]. Rahman, Atiqe Ur, et al. "An intelligent multiattribute decision-support framework based on parameterization of neutrosophic hypersoft set." Computational Intelligence and Neuroscience 2022 (2022).

[18]. Zulqarnain, Rana Muhammad, et al. "Aggregation operators for interval-valued intuitionistic fuzzy hypersoft set with their application in material selection." Mathematical Problems in Engineering 2022 (2022).

[19]. Hema, R., R. Sudharani, and M. Kavitha. "A Novel Approach on Plithogenic Interval Valued Neutrosophic Hyper-soft Sets and its Application in Decision Making." Indian Journal of Science and Technology 16.32 (2023): 2494-2502.

[20]. Siddique, Imran, et al. "Multicriteria decision-making approach for aggregation operators of pythagorean fuzzy hypersoft sets." Computational Intelligence and Neuroscience 2021 (2021).