Exploiting Graphics Processing Units to Speed Up Subgraph Enumeration for Efficient Graph Pattern Mining GraphDuMato

Authors :

Mohammed Husainat

Address :

School of Computing, Applied Science University, Bahrain

Abstract :

Subgraph selection involves searching an input graph for subgraphs with a certain attribute. Graph pattern mining (GPM) relies on this technique, despite its computing complexity and rapid growth. Problems with uncoalesced access to memory, separation, and strain unbalance make efficient subgraph identification on GPUs a huge problem, given GPUs' success in speeding up operations across multiple industries. It is surprising that these challenges have not received sufficient attention in earlier research. This work presents new methods for effectively building and running subgraph enumeration on GPUs. Optimization of computational resource usage is achieved by combining a warp-centric design with a Depth first search (DFS) style approach. Memory efficiency, execution divergence, and GPU activity parallelization could all be enhanced by integrating these two methods. An affordable load balancing level is also incorporated for the purpose of dispersing work among thread warps, which further decreases GPU idleness. The GraphDuMato system facilitates the utilization of GPM methods with its intuitive application programming interface (API). Testing proves that GraphDuMato can outperform state-of-the-art GPM algorithms on a regular basis and may mine subgraphs with up to twelve trees.

1.Introduction

Social media [1] as well as biological network [2] studies utilize graph pattern mining. The main attention is on important graph subgraph patterns. Sequential subgraph enumeration across an input graph searches for subgraphs that correspond to a graph property. Greater subgraph mining requires more memory and processing power [3]. The Bio-disease 1 biological dataset has 516 nodes with 1,2 thousand edges. An estimated 112 billion 10-node subgraphs in this collection. Storing these subgraphs would take 4 terabytes of RAM based on a 4-byte numeric for each vertex [4].

To enumerate subgraphs, the subgraph extension process is essential. Subgraph s is merged with k vertices using a set of extension (vertex ids) obtained from the adjacency of edges in subgraph s. The study has added k+1 nodes to your subgraph. The subgraph extension of s1 produces four extended subgraphs using induced subgraphs s1 and s2, while s2 produces six. Given the potential for extraordinarily long execution durations owing to the massive number of subgraphs requiring analysis, efforts are underway to develop massively parallel architectures [5]. Particular GPM methods have been designed for parallel implementation in the context of shared and dispersed memory devices [6]. In most cases, these techniques will reduce the memory and processing requirements by modifying . Even while new algorithms have shown promising performance in some contexts, their development has been a lengthy and difficult process [7].

The reasoning behind this is that different GPM algorithms may be able to benefit from different sets of constraints. Because of this need, GPM systems were created. These systems can support certain graph properties, which allows for subgraph listing and the application of specific GPM algorithms. [8] The combination of GPM systems' programmability and performance is ideal because it strikes a good balance between the two. GPUs speed up a lot of programs [9]. The architectural efficiency of GPUs is severely constrained by subgraph enumeration parallelization approaches. These limitations are concerned with memory noncoalescence, divergences, and imbalances in load. Pangolin is the most compact GPU-based GPM system [10].

The downside is that it uses a lot of memory and wasn't designed or developed to make the most of the GPU's processing power. This is achieved by reducing load imbalance, enhancing the memory access structure, and avoiding divergence. Then, we will discuss in detail the main challenges of concurrent subgraph identification on GPU that were found in this study [11].

The first hurdle that needs to be surmounted is the enormous memory demand that enumeration causes. The combinatorial explosion of subgraphs could occur as the enumeration progresses because subgraph allowance depends on integration a subgraph with its extensions. The BFS technique, used in Pangolin [12], is an outstanding optimal for parallel subsection enumerations since it consistently displays parallelisms when exploring adjacency lists. This style was created by Pangolin. Conversely, all states linked to extended subgraphs are materialized by BFS. And as this method's memory consumption grows exponentially with subgraph size, it can only be used to enumerate very small subgraphs. In contrast, the memory requirement is reduced by using the depth-first search (DFS) style technique, as only a small fractions of the states are retained during enumeration. Though, the GPU's parallel performance might be negatively affected by this approach's strided and irregular memory demands [13].

The second issue arose because the enumeration procedure is fundamentally erratic. Using subgraph-centric processing, which treats subgraphs as separate operations, the latest generation of GPM systems enables concurrent subgraph enumeration [14]. Different warp threads access strided memory locations or graph parts based on the subgraph they are processing, causing memory decoalescence and inefficient memory bandwidth utilization. The adjacency lists' differing widths and processing costs cause execution divergence in scale-free graphs. Thus, GPU usage is inefficient. The third issue is load imbalance, which arises from the unpredictable cost of subgraph research. This makes cost estimation difficult. Even with subsections s1 and s2 assigned to separate threads for parallelism, idleness is likely. Some threads finish early. Address these three challenges to successfully deploy GPM techniques on GPUs in this research.These strategies are presented in greater detail below. The following is a summary of our contributions:

• To demonstrate the importance of subgraph enumeration in graph pattern mining (GPM) and its computational complexity and rapid evolution problem in evaluating complex data structures.
• To discuss the challenges of subgraph enumeration on Graphics Processing Units (GPUs), such as uncoalesced memory access, divergence, and load imbalance, which reduce performance and scalability.
• To emphasize the need for creative solutions to GPU-accelerated subgraph enumeration concerns in the literature.
• To use depth-first search style search (DFS-wide) and warp-centric architecture to improve GPU subgraph enumeration efficiency and scalability to optimize computational resource utilization and overcome inherent challenges.

An overview of the research that was done is provided below. A thorough review of the literature and research methodologies in use is done in the second section. Section 3 contains a description of Preliminaries and problem statement. Section 4 provides a description of the research plan, research methods, and processing procedures. Section 5 contains a description of the findings analysis. The main conclusion and upcoming work are covered in the sixth section.

2. Literature Survey

Guo et al. [16] presented the Subgraph mining and network motif finding require subgraph enumeration. GPUs parallelize subgraph enumeration, while set intersection procedures take up to 95% of processing time. This article reuses these procedures' results to prevent recalculating. Generate a reusable plan using a reuse discovery technique, then execute the plan to provide subgraph enumeration results using a new reusable parallel search strategy. The GPU implementation can outperform state-of-the-art GPU methods by 5 times.

Dhote et al. [17] shown by offering end users constant support, distributed cloud technologies enhance mobile healthcare applications. Data storage and reorganization inefficiencies can still hasten the demise of services and recommendations. Improving data organization and mining while reducing errors is the goal of the Distributed Data Analytics Organization Model. To make sure that service deployment goes smoothly, the model employs federated learning, iterative learning in real-time, and state management. Using several circumstances, we assess how well this model performs.

The biggest issue of graph analytics is subgraph enumeration, reported by Yang et al. [18], which entails finding every query graph on a vast data graph. This work introduces HUGE, a distributed subgraph enumeration system. Huge has a revolutionary two-stage execution mode with lock-free and zero-copy cache, a BFS/DFS-adaptive scheduler to reduce memory consumption, two-layer intra- and inter-machine load balancing, and an optimiser to compute an advanced execution plan without constraints. Has a mixed communication layer. Huge can speed up distributed subgraph enumeration with confined memory.

3. Preliminaries

let's pretend for the purpose of simplicity that there are no labels and no directed graphs; nonetheless, our methodologies can be modified to include directed graphs and features with labels. The symbols 𝑉 (𝐺′) for vertices and 𝐸(𝐺′) for edges in a graph G are as follows.

. The symbols 𝑉 (𝐺′) for vertices and 𝐸(𝐺′) for edges in a graph G are as follows. The study are primarily concerned with counting induced subgraphs, which are subgraphs S where (𝑣𝑖, 𝑣𝑗) ∈ 𝐸(𝑆) iff (𝑣𝑖, 𝑣𝑗) ∈ 𝐸(𝐺′), for every 𝑣𝑗 ∈ 𝑉 (𝑆). The process of exploring a graph is described by incremental visits to the neighborhoods of vertices, which are referred to as traversals (Definition 1). (Definition 2) Induced traversal refers to the process of using a traversal to generate an induced subgraph from its vertices. Typically, algorithms of GPM begin their traversal of the graph at each vertex or edge. There are two main types of traversal strategies: breadth-first search (BFS) and depth-first search (DFS). Two traversals are considered to have found an automorphism (Definition 3) when they identify a shared set of vertex sets among subgraphs.

Definition 1:The neighborhood of a subgraph 𝑆 𝑖n a graph 𝐺′ is determined by the formula 𝑁(𝑆) = {𝑣 ∈ 𝑛𝑒𝑖𝑔ℎ𝑏𝑜𝑢𝑟𝑠(𝑢) | 𝑢 ∈ 𝑉 (𝑆)} \ 𝑉 (𝑆), where 𝐺′ is the graph and S is a subgraph of 𝐺’.

Definition 2 states that a set of traversal of 𝑘’ exclusive vertices in a graph 𝐺′ (𝑡𝑟 ⊆ 𝑉 (𝐺′)) that stores the order in which each vertex 𝑣 ∈ 𝑡𝑟 is visited in 𝐺′. Existing edges among the vertices accompany an induced traversal.

Definition 3: A bijective function 𝑓 ∶ 𝑉 (𝐺′) → 𝑉 (𝐻) is an isomorphism between two graphs G’ and 𝐻 if and only if, for every edge (𝑣𝑖, 𝑣𝑗) ∈ 𝐸(𝐺′), (𝑓(𝑣𝑖), 𝑓(𝑣𝑗)) ∈ 𝐸(𝐻).

Automorphisms are graphs 𝐺 ′and 𝐻 that are isomorphic to each other, defined as 𝑉 (𝐺′) = 𝑉 (𝐻).

If a graph G' and a set of traversals T create the same inspired traversal trind, the definitive option is the single T traversal that can reach G' trind with the allowed visited order of vertices.By limiting themselves to canonical possibilities, GPM algorithms eliminate wasteful computation by ensuring that no two exploration traversals end up at the same induced traversal. It is possible to transform canonical candidates into a distinct representation known as a canonical representative, or pattern, in this context. Canonical labeling is a common procedure in GPM methods for subgraph classification; it involves converting an induced traversal to its canonical representation.

4. Proposed Methods for Mining GPU Graphics Patterns Efficiently

Graph pattern mining techniques that make good use of graphics processing units (GPUs) are detailed here. In this first section, the study provides a brief introduction to GraphDuMato, our technology that enables the GPU application of GPM algorithms at a great level. After that, the study shows that the way plan is to lessen memory request, boost memory combination and separations, and lessen load imbalance using the GraphGraphDuMato execution process.

GraphDuMato Process for Execution

Figure 1 shows the GraphDuMato execution pipeline, which develops GPM procedures founded on the listing function E using the filter-process approach. Decisions are represented by diamonds in Figure 1, while process steps are represented by circles. E(G, tr, k, P) is invoked first in order to iterate over all traversals of size k satisfying the condition P. This extension of the original traversal tr allows the study to begin. The control phase applies the termination condition (|tr| = 0) by first using tr as an input. The study's Control phase decides whether to continue subgraph enumeration when the traverse is not empty or halt it when it is.

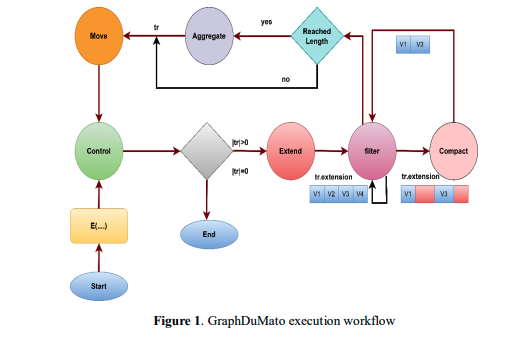
As enumeration continues, the Extend phase calculates extensions from the current traversal (|tr| < k) (Figure 1). Adjacency of traversal vertices determines these probable extensions in the area around the current subgraph (Def.1). Extend extends the current traversal and any subsequent extensions. After then, application-specific semantics can pick subgraphs with anti-monotonic property P (|tr| < k) during the Filter phase. Property P can determine if a subgraph has cliques. Passing invalid extensions that do not satisfy property P does this. To guarantee property P, many filters can verify different circumstances. Filter produces valid extensions and current traversal. The Filter's output may have several invalidated or erased extensions, like v2 and v4 in Figure 1. Because the following Filter may filter or validate invalid data, this array of non-contiguous legitimate extensions may drastically influence performance. The optional Compact step after each Filter consolidates valid extensions into a contiguous memory/array. The enumeration output A (|tr| = k in Eq. 1) receives data that approaches the target number of vertices as the traversal size after all Filter/Compact stages. Traversals for pattern counting, buffering, or counting achieve this in the Aggregate phase. The Aggregate step is skipped if the vertices objective is not met. Enumerating subgraphs forward or backward is decided in the Move phase before continuing. The traversal can process unprocessed extensions using a recursive call. Following all extensions of the current traversal, recursion return lets the algorithm process smaller traversals. The Move's updated traversal should close Figure 1's cycle and restart the operation at the Control. We enumerate warps separately and allocate work warp-centrically. As a warp executes, threads enumerate the same traversal alternating between SIMD and SISD phases. Below, we'll discuss GPU-based GPM algorithms' memory demand, execution irregularities, and load imbalance reduction strategies. From design to implementation, the study covers the entire execution procedure. A simple API is also highlighted in the study.

b. Exploring Subgraphs Across DFS

The research presents a new method for exploring subgraphs throughout DFS that toggles between BFS and DFS phases to allow regular subgraph enumeration on GPU. Figure 2 depicts the combined processes of BFS and DFS in a single iteration, as well as an overview of the DFS-wide exploration methods. Each DFS-wide intermediate stage is stored in a separate TE (Traversal Enumeration) array. The current traversal's vertex identifiers are kept in TE.tr, whereas the extensions formed during enumeration are maintained in TE.ext.

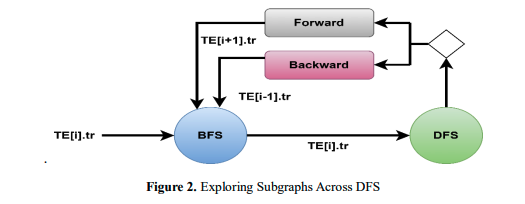
A traverse is used to begin the enumeration in Figure 3. The extensions are efficiently produced and stored in a contiguous array (𝑇 𝐸[𝑖]. 𝑒𝑥𝑡) by the BFS phase and 𝑇 𝐸[𝑖].𝑡𝑟, which will be saved in a temp file. The DFS moves back or forward in the enumeration while receiving tr and extensions, depending on their length. Keep in mind that the DFS phase will improve memory efficiency by accessing extensions in a contiguous region that is likely cached, both in forward and backward directions. When the traversal size exceeds the target, the enumeration process switches between BFS and DFS phases. Since the study wishes to count traversals 𝑡𝑟 = {𝑣0, 𝑣1}, the steps taken in the BFS and DFS phases during one DFS-wide iteration are illustrated in Figure 3. A warp replicates the vertices in the current traversal's adjacency lists to extensions during the BFS phase (step 1), and only the distinctive extensions which are not in 𝑡𝑟 (step 2) are kept. Step 3 of the DFS phase involves generating extensions; step 4 involves increasing the current traversal and consuming a vertex (v2) from extensions.

	𝑨𝒍𝒈𝒐𝒓𝒊𝒕𝒉𝒎 𝟏: Move Primitive1
	𝑰𝒏𝒑𝒖𝒕: TE1 (traversal and extensions data), genedges1 (bool for generating edges)
	𝑶𝒖𝒕𝒑𝒖𝒕: Updates TE1 to the next traversal
	𝒊𝒇 traversal size1 != target size and extensions exist 𝒕𝒉𝒆𝒏
	get next extension ext1
	append ext1 to traversal in TE
	if genedges1: generate edges for extended traversal
	𝒆𝒍𝒔𝒆 backtrack to previous traversal
	𝒊𝒇 no more traversals 𝒕𝒉𝒆𝒏
	get new traversal from global queue
				

---

centered on warp Algorithm 1's Move executes the DFS phase, while GraphDuMato's warp-centric Extend phase implements the BFS phase. In traversal enumeration, move can either advance or regress the warp. To determine whether traversal edges need to be constructed during enumeration, TE and genedges are required. As a method for extracting traditional representations from subgraphs, pattern counting makes use of traversal edges and connectivity data. As enumeration progresses, the Move phase increasingly produces edges if needed. If the current traversal is still greater than the starting limit and the collection of expansions is not empty, the warp will consume one extension and extend the current traversal to advance in the enumeration. Induce is a stage of the SIMD algorithm that, if necessary, generates extended traversal edges by reusing the current ones. If the current traverse does not have an empty present extensions set or is larger than the size limit, warp will move backward in accordance with the enumeration. Once the present traversal has been enumerated, the warp retrieves a fresh one from a worldwide queue.Move is the only costly induce functional and SISD phase since all warp threads use the same traverse to refresh data.

c. Optimal Warp-Centered Filter-Process

In this part, the study will go over the filter-process workflow's GraphDuMato phases and how they were designed and implemented using a warp-centric approach. By using this paradigm want to reduce the performance gap between our non-standard algorithms and take advantage of the DFS-wide strategy's parallelism and regular memory access.

	𝑨𝒍𝒈𝒐𝒓𝒊𝒕𝒉𝒎 𝟐: Extend Primitive1
	𝑰𝒏𝒑𝒖𝒕: TE1 (current traversal), start, end (range of vertices to consider)
	𝑶𝒖𝒕𝒑𝒖𝒕: True if new extensions generated, updates TE1 with new extensions
	𝒊𝒇 extensions already generated 𝒕𝒉𝒆𝒏
	𝒓𝒆𝒕𝒖𝒓𝒏 False
	𝒇𝒐𝒓 each vertex id1 in given range 𝒅𝒐
	𝒇𝒐𝒓 each neighbor e1 of vertex 𝒅𝒐
	𝒊𝒇 e1 not in traversal and not in extensions 𝒕𝒉𝒆𝒏
	add e1 to extensions
	𝒓𝒆𝒕𝒖𝒓𝒏 True
					

---

In algorithm 2, Graph processing tools like the GPM method, which use GraphDuMato primitives to access the TE data structure, are quite effective. Filter, compact, and aggregate are its three primary stages. The filtering process iteratively rejects extensions that fail to satisfy a property P. The TE data structure is accessed in this warp-centric phase using GraphDuMato primitives. An optional phase called compact finds the current traversal's extensions set, removes invalid locations from there, and then shortens the traversal. Using compaction to remove invalid places lowers the cost of successive filter calls. Using intra-warp communication primitives like any sync and ballot, GraphDuMato efficiently implements this function with a focus on warps. The thread warp responsible for producing the actual GPM algorithm outputs is aggregated when it has derived traversals with k vertices. The three aggregating primitives provided by GraphDuMato are sum, pattern, and store. Since it be dependent on counting the existence of canonical legislatures through k vertices, the aggregate pattern presents the greatest challenge for GPU implementation of primitives. This is carried out in a warp basis, with a counter incremented, and every subgraph with k vertices converted to its canonical representation.

	𝑨𝒍𝒈𝒐𝒓𝒊𝒕𝒉𝒎 𝟑: Filter Primitive1
	𝑰𝒏𝒑𝒖𝒕: TE1 (traversal and extensions), P1 (property function), args1 (arguments for P)
	𝑶𝒖𝒕𝒑𝒖𝒕: Updates extensions in TE1 by invalidating those not satisfying P1
	𝒇𝒐𝒓 each extension ext1 in TE1 𝒅𝒐
 	𝒊𝒇 P1 (TE1, ext1, args1) is False 𝒕𝒉𝒆𝒏
 	invalidate ext1

The approach to canonical relabeling is Nauty, which Pangolin and other GPM systems use for performing graph isomorphism on CPU in algorithm 3. The authors implemented GPU canonical relabeling. The dictionary they generate takes a traversals tr containing k vertices and its bitmap edge representation. Respectively warp can use local counts for canonical representation while using less RAM because no counters are wasted. The aggregate count primitive is used for clique counting GPM algorithms that produce pattern counts. After reducing warps' CPU counting, the global counting is generated, and every warp generates its own count that avoids races. Subgraph searching uses rudimentary aggregate store stores to analyze k-vertice subgraphs As soon as an examined subgraph with k vertices is created, the array buffer stores its connectivity bitmap.

	𝑨𝒍𝒈𝒐𝒓𝒊𝒕𝒉𝒎 𝟒: Clique and Motif Counting1
	𝑰𝒏𝒑𝒖𝒕: TE1 (data structure for traversals/extensions)
	𝑶𝒖𝒕𝒑𝒖𝒕: Counts number of cliques or motifs of size k1
	𝑺𝒕𝒆𝒑 𝟏:Clique Counting1
	𝒘𝒉𝒊𝒍𝒆 more traversals exist 𝒅𝒐
	extend traversal with neighbors of first vertex
	filter extensions lower than last added vertex (non-canonical)
	compact extensions array
	filter extensions that don't form a clique
	𝒊𝒇 traversal has k1 vertices 𝒕𝒉𝒆𝒏
	count the clique
	move to next traversal
	𝑺𝒕𝒆𝒑 𝟐:Motif Counting1
	𝒘𝒉𝒊𝒍𝒆 more traversals exist 𝒅𝒐
	extend traversal with neighbors of all vertices
	filter non-canonical extensions
	𝒊𝒇 traversal has k1 vertices 𝒕𝒉𝒆𝒏
	count motif pattern
	move to next traversal						

---

In algorithm 4, cliques are counted. Vi and vj for every j in V(C) are members of the subgroup of size k in the set E(C). The clique counting issue takes a graph G and attempts to determine how many cliques there are with k vertices. Subgraphs sharing a pattern can be located by employing "lique counting" approaches. In the Extend phase, the array of extensions for the traversal is created from the neighbors of individual vertices. At least one clique extension must accompany each vertex in the traverse. Utilizing this idea, the [EX] call in line 3 of Algorithm 4 gathers current extension from the neighbors of the first vertex in the traverse ([0,1]). Extensions below the final vertex are invalidated by the function [FL] on line 5, which is part of the canonical candidates. The array of extensions is compacted by [CP] at line 6. Line 7 keeps on removing extensions that do not contain cliques by utilizing the notation [FL]. Valid extensions must be attached using the clique special method to each traverse vertex. A traversal and an extension are passed to the lower and is clique functions, which then return true or false, respectively. Lastly, one may use the [A1] counter to aggregate the length of a given array of expansions for traversals with k vertices.

d. Load Balancing on Warp Levels

An asynchronous workload redistribution mechanism on the CPU can alleviate load imbalance among warps caused by the cost of enumerating unique traversals. This approach uses data about warp levels to make judgments and runs all of its procedures on the central processing unit. In a consistent state, the CPU notifies the GPU of load balancing by setting a flag and pausing warp execution. We suggest a rebalancing condition that would cause work redistribution if the quantity of active warps is resolute to be less than a certain edge

By classifying warps as either active participants or passive observers, the redistribute method is able to achieve load balance. The central processing unit (CPU) checks warp activity and redistributes tasks while the graphics processing unit (GPU) is running. Altering the scheme's redistribute and balance steps to incorporate other strategies is a breeze. For every GPM algorithm that uses the counting of induced subgraphs, GraphDuMato's workflow can stand in for it. Functions [CT] and [MV] allow the runtime to examine execution termination conditions during these stages. The four steps—extend, filter, condense, and aggregate—make GPU application-specific semantics representation simple and efficient. Until the termination condition is met, algorithms run through fresh traversals.

5. Result and discussion

Graph pattern mining methods on GPUs are the focus of this paper's evaluation of suggested optimization techniques. It evaluates Graph GraphDuMato Depth-First Search (GDM DFS) and Graph GraphDuMato Warp-Centric (GDM WC) based on parameters like global load transactions and instructions per warp. When compared to GDM DFS, the GDM WC method improves the execution pattern, which in turn increases the number of instructions per warp by 3.8x to 13.3x. By facilitating more coordinated memory access patterns, the WarpCentric DFS-Wide method lessens the overall number of memory transactions. A criterion of 40% for clique counting and a threshold of 10% for motif counting are used by 172,032 threads to determine the ideal load balancing threshold. When comparing GDM WC and GDM OPT, the optimized GraphDuMato GPU implementations achieve speedups of 65x for motif counting on the Citeseer dataset with k = 8. The GPU studies were carried out on TITAN V and NVIDIA Tesla V100 GPUs using CUDA 10.1 and CUDA 11. Highlighting the advantages of using GPUs for speeding up graph pattern mining algorithms, the results show that the suggested optimization techniques are helpful in boosting execution and memory efficiency for subgraph enumeration on GPUs.

a. Dataset Description

For machine learning and network analysis, the Citeseer dataset[23] contains citation networks. Besides source information, issue year, and document title, it provides nodes for computer science papers and edges for citations. A directed graph with dataset nodes and edges lets researchers study citation patterns, publication influence, and other network properties. Popular uses of Citeseer include links prediction, community discovery, and reference network node classification. Researchers use this dataset to develop and test methods for citation networks and intellectual document analysis.

a. Execution Time Speedup

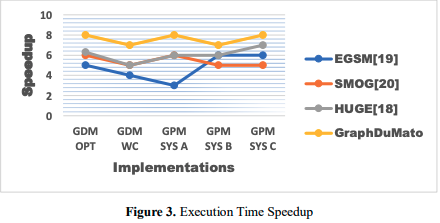
In figure 3, execution time speedup is a key indicator for comparing GraphDuMato to other GPU-based Graph Pattern Mining (GPM) systems. Compare the time it takes the GraphDuMato GPU implementations (GDM OPT, GDM WC) to execute on a reference system like a state-of-the-art GPM system. If the speedup number is high, GraphDuMato GPU implementations outperform reference GPM systems. GraphDuMato beats state-of-the-art GPM solutions in efficiency, performance, and computational throughput with a greater speedup value. One of the most essential measures for evaluating GraphDuMato's optimization and GPU acceleration strategies is speedup, which compares its graph mining performance to competitors. GraphDuMato's design, memory optimizations, load balancing techniques, and parallelization methods speed up GPU-accelerated graph pattern mining. Compared to competing GPM systems, GraphDuMato is faster and more scalable. Graph mining algorithm efficiency improved. According to its speedup data, GraphDuMato beats modern graph pattern mining methods, demonstrating system optimizations

c. Size of Enumerated Subgraphs

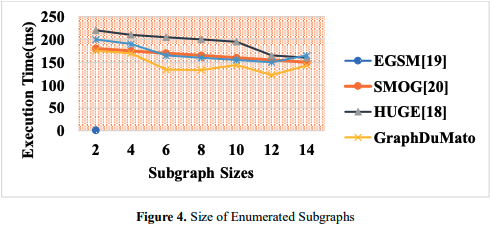
As seen in Figure 4, GPUs help Pattern Mining handle larger subgraphs, especially those with 12 vertices. Utilizing these properties shows its efficiency, adaptability, and effectiveness in complex graph patterns. Due to its effective design and architecture, GraphDuMato handled larger subgraphs' computing demands without issue. Thus, network mining for patterns becomes more efficient, yielding more complete and useful results. It also boosts productivity and lets you analyze complex graph topologies. Because it supports larger subgraphs, GraphDuMato excels at complicated graph pattern mining. Users can gain insights from complex data representations with this feature.

d. Optimal Load Balancing Threshold

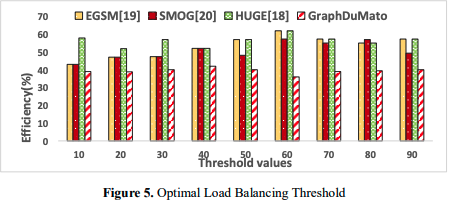
Assuming the information in Figure 5 In GraphDuMato's GPU-based GPM method, the Optimal Balanced Load Threshold is a key parameter that determines when the computational workload is divided between the GPU thread warps through the process of load balancing. Efficiently using GPU resources with little overhead is crucial. It is crucial to set the threshold to the right value for the system to run at its best with little unnecessary overhead, adaptability, and efficient job distribution. When processing needs and workloads change in real timeinstantaneously, GraphDuMato can adjust the threshold value accordingly. In conclusion, the optimal load balancing threshold in GraphDuMato boosts system performance by efficient job distribution among GPU thread warps.

6. Conclusion and Future work

To circumvent these issues, GraphDuMato has created GPU-based GPM, which offers novel approaches to running GPM algorithms on GPUs. GraphDuMato makes GPU graph pattern mining more efficient and scalable by reducing memory requirements, improving memory access patterns, limiting divergences, and balancing computational workloads. With its warp-centric layout, lightweight load distribution, and DFS-wide subgraph search, GraphDuMato is able to mine larger subgraphs more efficiently than prior GPM systems. Despite its advancements, GraphDuMato still has certain drawbacks. The dataset and subsection sizes affect the processing time of GPM techniques. In spite of being faster and more scalable than existing solutions, the study may find that GraphDuMato need some more improvements for particular applications or datasets. There may be more advanced capabilities that would enhance GraphDuMato's utility in GPM applications that are currently absent from the present version. Future iterations of GraphDuMato's load balancing technology will provide fine-grained asynchronous task redistribution. Efficiently managing tasks without requiring GPU kernel restarts maximizes GPU utilization. The organization is considering utilizing GraphDuMato across multiple GPUs to speed up processing, which is particularly important for big datasets and complicated graph mining procedures. Future work could also focus on implementing a fault resilience layer to guarantee GPM continuity and reduce long runs. These updates will make the GraphDuMato GPM platform more robust, scalable, and efficient, making it suitable for a wider range of datasets and uses.

References :

[1]. Bouhenni, Sarra, et al. "A survey on distributed graph pattern matching in massive graphs." ACM Computing Surveys (CSUR) 54.2 (2021): 1-35.

[2]. AlMasri, Mohammad Abed Alnaser. Accelerating graph pattern mining algorithms on modern graphics processing units. Diss. University of Illinois at Urbana-Champaign, 2022.

[3]. Rao, Gengyu, et al. "Intersectx: an efficient accelerator for graph mining." arXiv preprint arXiv:2012.10848 (2020).

[4]. Chen, Jingji, and Xuehai Qian. "DecoMine: A Compilation-Based Graph Pattern Mining System with Pattern Decomposition." Proceedings of the 28th ACM International Conference on Architectural Support for Programming Languages and Operating Systems, Volume 1. 2022.

[5]. Arduengo García, Ana. Locality analysis and its hardware implications for graph pattern mining. BS thesis. Universitat Politècnica de Catalunya, 2023.

[6]. Ferraz, Samuel, et al. "Efficient Strategies for Graph Pattern Mining Algorithms on GPUs." 2022 IEEE 34th International Symposium on Computer Architecture and High Performance Computing (SBACPAD). IEEE, 2022.

[7]. Li, Lei, et al. "Semi-supervised graph pattern matching and rematching for expert community location." ACM Transactions on Knowledge Discovery from Data 17.1 (2023): 1-26.

[8]. Lin, Zhiheng, et al. "Exploiting Fine-Grained Redundancy in Set-Centric Graph Pattern Mining." Proceedings of the 29th ACM SIGPLAN Annual Symposium on Principles and Practice of Parallel Programming. 2024.

[9]. Qi, Hao, et al. "PSMiner: A Pattern-Aware Accelerator for High-Performance Streaming Graph Pattern Mining." 2023 60th ACM/IEEE Design Automation Conference (DAC). IEEE, 2023.

[10]. Talati, Nishil Rakeshkumar. Optimizing Emerging Graph Applications Using Hardware-Software CoDesign. Diss. 2022.

[11]. Cui, Limeng, et al. "Deterrent: Knowledge guided graph attention network for detecting healthcare misinformation." Proceedings of the 26th ACM SIGKDD international conference on knowledge discovery & data mining. 2020.

[12]. Azad, Ariful, et al. "Evaluation of graph analytics frameworks using the gap benchmark suite." 2020 IEEE International Symposium on Workload Characterization (IISWC). IEEE, 2020.

[13]. Yuan, Lyuheng, et al. "T-FSM: A task-based system for massively parallel frequent subgraph pattern mining from a big graph." Proceedings of the ACM on Management of Data 1.1 (2023): 1-26.

[14]. Zeng, Li, Lei Zou, and M. Tamer Özsu. "SGSI–A Scalable GPU-friendly Subgraph Isomorphism Algorithm." IEEE Transactions on Knowledge and Data Engineering (2022).

[15]. Qiu, Linshan, et al. "Accelerating Biclique Counting on GPU." arXiv preprint arXiv:2403.07858 (2024).

[16]. Guo, Wentian, Yuchen Li, and Kian-Lee Tan. "Exploiting reuse for gpu subgraph enumeration." IEEE Transactions on Knowledge and Data Engineering 34.9 (2020): 4231-4244.

[17]. Dhote, Sunita, et al. "Cloud computing assisted mobile healthcare systems using distributed data analytic model." IEEE Transactions on Big Data (2023).

[18]. Yang, Zhengyi, et al. "Huge: An efficient and scalable subgraph enumeration system." Proceedings of the 2021 International Conference on Management of Data. 2021.

[19]. Sun, Xibo, and Qiong Luo. "Efficient GPU-Accelerated Subgraph Matching." Proceedings of the ACM on Management of Data 1.2 (2023): 1-26.

[20]. Wang, Zhibin, et al. "SMOG: Accelerating Subgraph Matching on GPUs." 2023 IEEE High Performance Extreme Computing Conference (HPEC). IEEE, 2023.

[21]. Hussein, Rana, et al. "GraphINC: Graph Pattern Mining at Network Speed." Proceedings of the ACM on Management of Data 1.2 (2023): 1-28.

[22]. Gui, Chuangyi, et al. "Sumpa: Efficient pattern-centric graph mining with pattern abstraction." 2021 30th International Conference on Parallel Architectures and Compilation Techniques (PACT). IEEE, 2021.

[23]. https://networkrepository.com/citeseer.php