Application-Oriented Pattern Analysis Utilizing the SPTA Algorithm for Efficient Targeted Sequential Pattern Mining
Authors :
Ramya Devi and Ramachandran
Address :
Sri Ramachandra Medical College and Research Institute
Universite´ de Lyon, Ecole Normale Supe´rieure de Lyon, France
Abstract :
In the gaming business, esports, also known as competitive gaming, has ushered in a new age that has brought up some innovative issues. One of these challenges is determining the level of player competency based on their plans and talents. Using game traces from Rocket League, a one-of-a-kind "soccer with rocket-powered cars" game, this investigation focuses on the automatic recognition of skill shots, an essential component of player performance. Challenges arise for classic pattern matching algorithms due to the unique characteristics of each skill performance. A Player Skill Modeling through Data-Centric Patterns (PSM-DCP) strategy that uses pattern mining and supervised learning techniques offers a solution to this issue. To highlight the potential of our system for player modeling shows that it can efficiently detect a wide variety of Rocket League abilities and shots. Also confirm the efficacy of this technique by conducting a comprehensive set of tests, which reveals that it is able to effectively differentiate and evaluate skillshots. The study results have a wide range of implications for various applications within esports. These applications include the improvement of match-making algorithms, the provision of assistance to game commentators in the form of insightful assessments, and the development of learning systems that are intended to improve player abilities. This study not only tackles the unique context of Rocket League, but it also offers a framework for exploiting data-centric techniques in esports analytics. This allows for additional developments and applications in competitive gaming, which opens up new paths for possibilities.
Keywords :
Sequential Pattern Mining; Application-Oriented Pattern Analysis; SPTA Algorithm; Real-World Uses; Pattern Analysis; Target Sequences; Querying Sequences.
1.Introduction
A widely recognized topic in the data analysis arena, frequently occurring pattern mining (FPM) [1] aims to find all valuable and common patterns in given user-provided material. With FPM, you may find out how often a pattern appears by comparing its database occurrence to the minimum support threshold (minsup) that you choose. Assuming the pattern is common, we can conclude that its constituent parts are disorganized. Since the order of appearance in the documentation of transactions is not considered by FPM, <𝐴, 𝐵> and <𝐵, 𝐴> are equivalent [2]. Several services make use of FPM in practice, and it aids in making good judgments and finding good solutions by analyzing different types of data. Consider this breakfast establishment: The research reveals two recurring themes in the data: firstly, that most purchasers engage in both kinds of purchases; and secondly, that this is the case for the vast majority of customers.
Bread and milk stand out as the morning store's flagship products due to these two trends. More customers will purchase milk and bread at once if the store owner stacks them. This link cannot be determined if the study merely collects the pattern[3]; this is based on the actual survey findings. But repeat buyers of bread are more inclined to also purchase milk. Perhaps this is due to the fact that bread is more commonly thought of as a basic food and milk more as a drink. Assuming this to be true, some shoppers will buy milk alongside their bread. Actually, the unusual trend will show that very few customers buy milk alone or buy bread after buying milk. According to the numbers presented above, the store can charge a bit more for bread deprived of increasing the price for both the bread as well as milk combination.
Choosing the option can definitely improve sale promotion. The example of a basic breakfast store exemplifies the problem with FPM: it ignores the relative placements of goods in the transaction records. For these problems, sequential pattern mining (SPM) [4] was proposed as a solution. Compared to FPM, SPM can definitely find more important and useful patterns. When SPM makes into account of the connection between the positions of each items in the transaction data, it produces two separate patterns for <𝑬, 𝐵> and <𝑵, 𝐵>. Academics in the field have to come up with a slew of new algorithms and ways to increase production [5]. Furthermore, some scholars focus on specific study contexts in order to tackle real-world difficulties in different settings. For example, click-stream analysis on websites, DNA analysis in biology, and user behavior analysis in business [6].
To meet the format criteria of observed sequential patterns, closed, multi-dimensional, and overlapping sequential patterns have been studied. Traditional SPM algorithms detect sequential minsup patterns using frequency. Common transaction record sub-sequences are mined sequential patterns. To determine if a transaction database sequence is one-item or multiple-item, check its itemset. Practicality is often higher for large sequences [8]. A breakfast store model is studied. If a customer buys bread and milk simultaneously, the correct sequence is < (bread, milk)> instead of <(bread), (milk)>. After buying bread, the buyer buys milk if the first or second is accurate. SPM outperforms FPM in sequential pattern mining. SPM prioritises items by order of occurrence. Patterns <𝐴, 𝐵> and <𝐵, 𝐴> differ in SPM but are same in FPM, as previously described in the study. Their inefficiency with huge databases and query workloads is clear. Mining produces large random sequential patterns. This study identified top-𝑘 sequential patterns querying [9] and targeting sequential patterns algorithm. Primarily, it seeks the most important sequential patterns, and secondarily, the patterns people focus on. With targeted SPM, we can detect the consumer's habits without creating extra ones. Supermarkets handle a lot of transactions. To find pencil-related sequential patterns, exclude other patterns. Google and other search engines use concentrated sequential pattern queries [10]. Search results are returned when users type keywords on the browser's keyboard. Several frequency-based targeted SPM methods [11] are either too narrow or too generalizable. These techniques can find sequential patterns that meet requirements. Query itemset is last. Checking internet search and transaction logs is unrestricted. If they search for a website using a verb, researchers may not discover many results [12]. Instead of ending phrases, verbs frequently come before nouns and adjectives. Concentrating on one thing is foolish. These algorithms cannot search transactional data appropriately since they focus on sequential book and pencil purchases. SPTA (targeted sequential pattern mining) is introduced in this study to overcome these concerns by changing the target sequential pattern. The document includes UTFP, UPIP, USIP, and UIIP techniques plus a post-processing mechanism. The acronyms represent unpromising 𝑇-Extension, prefix item pruning, and 𝑍-Extension. The research gives the SPTA algorithm and variants on it using these pruning strategies.The main contribution of this paper is:
- Redefining target sequential pattern mining to address current issues.
- Utilizing support processing techniques saving all qualified target sequential patterns.
- Proposing SPTA algorithms for outcome complete set of target sequential patterns.
- Proposing UTFP to filter distinct transactions.
- Proposing UPIP and UIIP to decrease needless procedures in mining method.
- Experiments using real and synthetic datasets to show different optimized performance of different SPTA variants.
This is the structure that the remaining of the study surveys. Section 2 provides a concise overview of the relevant prior research. 3rd Section lays out the challenge of targeted sequential pattern mining and defines the terms that are important to the discussion. Section 4 then presents algorithm proposal, SPTA. In Section 5, the study describes and displays the experimental findings. 6th Section concludes with a future work.
2. Literature Survey
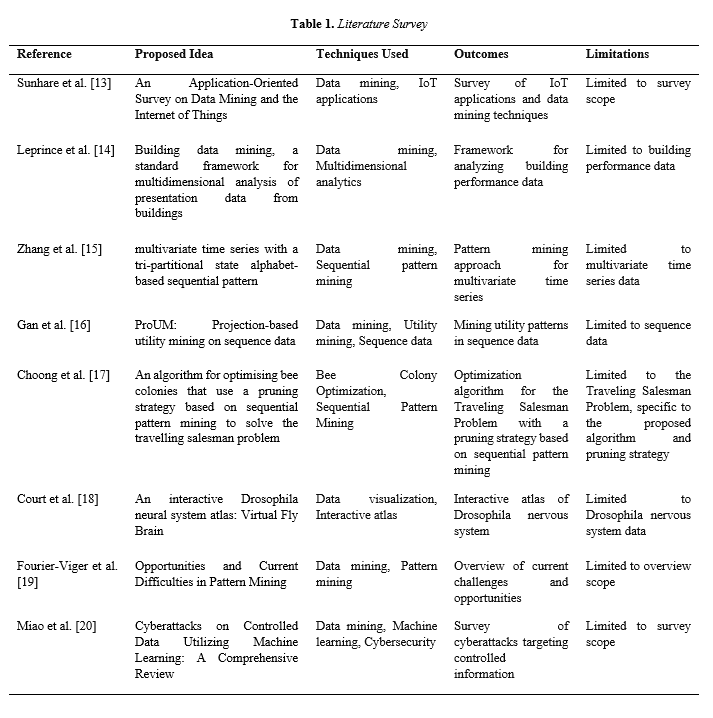
This review includes data mining studies and their applications. Data mining and Internet of Things surveys by Sunhare et al. are highlighted. A general framework for multidimensional building performance data analytics was developed by Leprince et al. A tri-partition state alphabet-based sequential pattern for multivariate time series was presented by Zhang et al. Project-based utility mining for sequence data was introduced by Gan et al. The Traveling Salesman Problem was solved by Choong et al. utilizing sequential pattern mining-based bee colony optimization. Fourier-Viger et al. reviewed pattern mining challenges and opportunities, Miao et al. examined machine learning-based cyber attacks on controlled information, and Court et al. created an interactive Drosophila nervous system atlas.
3. Preliminaries and Problem Definition
The following definitions define key-focused pattern mining terms and symbols. Their next definition of focused sequential pattern mining will be more formal. Emails are the paper's basic unit, and each item represents real-life products. The infinite set 𝐼 = {𝑖1, 𝑖2, · · ·, 𝑖𝑁} contains each unique object in a transaction database. Itemsets can be viewed as subsets of 𝐽, signified as X ‘(X '⊆ J). Note that the display will show ⋛𝑙𝑒𝑥, as each set is sorted alphabetically. As shown by the symbol | |, the size of an items X' is proportional to its number of items. Size is the sum of itemsets in a sequence, X', and length is the sum of its items, y. Uncertainty 𝑇1 is a sub sequence of 𝑇1 (𝑆 ⊆ 𝑇), then ∃ 𝑚, 1 ≤ 𝑘1 < 𝑘2 <... < 𝑘𝑚 ≤ 𝑛 such that ∀1 ,Given a sequence <(f' ),(f',b),(r )> and <(f',h),(f',b),(f' )>,S1 has a dimension of 3 and a length of 4. The investigation may conclude that 𝑆1 is a sub-sequence of 𝑆2 since it ⊆ 𝑆2. A sequence database identification A 1 <(𝑏), (𝑎, 𝑑)> is provided in Section 1. Two sets of elements contain (b),(a,b,m,d),(b),(f'). The set of three items is <(b),(a,b,c,d),(a,b),(e')> The outcome is <4 (b),(b,c,d,b),(e'),(m')>.
Definition 3.1: The identifiers of the sequence 𝑆 is represented in the set of tuples for a arrangement database D. This set's size, |D|, is equal to the database D's size. The sequence database that will be used as an example in the following definitions and ideas. It is clear that there are five sequences in this sample database, and that each sequence is assigned a distinct identification. The definition deals with support and minimal support. The support of an items or itemsets 𝐜 can be written as sup(e’ / J), where 𝑆 is an element of 𝑆 and 𝑌 is an element of D.
Definition 3.2: In the same way, sup(𝑆) = |𝑇 |𝑆 ⊆ 𝑇 ∧𝑇 ∈ D | can be used to represent the support values of a sequence 𝑆. The user specifies the minimal support in advance and calls it minsup. An item or sequence is referred to as frequent or sequential if and only if the subsequence of its size, sup(e' / 𝑆), is less than or equal to minsup. By setting minsup to 2, for instance, all items will be considered frequent. Due to the fact that sup(<(𝑔), (𝑎)>) = 3 ≥ 2, <(𝑔), (𝑎)> is a common sequential pattern.
Definition 3.3: (Mining for targeted sequential patterns and target sequential patterns). If you take a query sequence qs' and identify a target sequential pattern it of qs that fulfills qs’ ⊆ ts and sup(ts) > minsup, then the study can consider of qs’ as the common sub-sequence of ts. The ultimate goal of targeted sequential patterns algorithm is to find all potential target ordered patterns using the sequence of queries qs’, where minsup is set to 2 and qs’ = <(𝑎), (𝑏)>. It is not possible to have ts2 = <(𝑔), (𝑎), (𝑏), (𝑒)> since sup(ts2) = 1 < minsup, although ts1 = <(𝑔), (𝑎), (𝑏)> is the desirable sequential patterns of qs’. Using these ideas as a foundation, the study can formulate the targeted sequential pattern mining (SPTA) problem in the following way. Here is the problem: The goal of SPTA, given a database of sequences D, a query sequences qs’, and a minimal supporting threshold minsup, is to find all potential targeting sequential patterns ts of qs’ that meet the constraints qs’ ⊆ ts and sup(ts) > minsup.
4. Proposed Methodology
a. Methods for Definition and Pruning
Definition 4.1: The pattern-growth-based mining algorithm relies on extension as a crucial step. One kind of extension used in mining is the 𝑇-Extension, while the other is the 𝑎-Extensions. The 𝑆-Extension inserts a new item into the existing sequence by appending a new itemset to its end. Regarding 𝐽-Extension, it augments the current sequence by adding a new item to the last itemset. Adding these two expansions will undoubtedly cause the sequence to expand.
Definition 4.2: Targeted sequential pattern mining, as The study already established, does not have an algorithm. A post-processing strategy is required if the study intend to carry out this task using a conventional sequential pattern mining algorithm. As long as the sequential pattern was mined by SPM, this method will save the data. To find out if the created sequential pattern contains the question sequence, it scans through it. The study will save a pattern if it contains the query sequence; else, The study will filter it.
Definition 4.3: The study defines the current query item (qi) as the item that corresponds to the matching point in the query sequence in this study. Two flags are used to record the current position on the qi during the pattern growth. An itemset match position, abbreviated as IMatch, is the initial flag. The current location of the itemset that is matched to the query sequence can be recorded using IMatch. To find out where an item is in the itemset that is currently matching the query sequence, the study can use the second flag, which is IIMatch, which stands for item match position.There can determine that <(𝑏)> is the matching sequence and 𝑎 is qi, for instance, when there is a query sequence <(𝑏), (𝑎, 𝑑)> and a current pattern <(𝑏), (𝑏)>. Because of this, IMatch = 1 and IIMatch = 0.
Definition 4.4: Encoding a sequence 𝑦 as a bitmap returns [𝑆11 𝑆12..., 𝑆21...]. The study specifies the precise spot of the 𝑏-th itemset within the 𝑖-th sequence database as 𝑆𝑖𝑏. If 𝑏 and 𝑆𝑖 match, then 𝑆𝑖𝑏 is identical. A bitmap of the query sequence s = <(𝑎), (𝑏)> would be [0 0, 0 0 1 0, 0 0 1 0, 0 1 0 0]. As 𝑆2, 𝑆3, and 𝑆4 hold positions 2, 3, and 2, respectively, they can all match 𝑏. First, when does query sequence match? IMatch and IIMatch were begun at 0 in the research sequence. Every single iteration changes these two flags. Perfect matches are IMatch-length query sequences. After that, target sequential patterns can be preserved without modifying IMatch and IIMatch. II. When will IMatch and IIMatch updates arrive? The study compares an additional item of the current sequence to qi to assess if IMatch as well as IIMatch need updating. Both IIMatch and IMatch start at zero.
In this inquiry sequence, qi is the first item and the current sequencing is empty (<>). IMatch and IIMatch are set to 0 if long item 𝑏 does not match qi. Set IIMatch to 1 if qi matches item 𝑒. If it matches the query sequence's initial itemset, IMatch equals IIMatch + 1 and 0. The research compares query sequence qi to enlarged item qi as it progresses. If extended elements 𝑒 and qi are equivalent, update IIMatch to IIMatch + 1. If the query sequence's IMatch-th item equals IIMatch after the update, IMatch becomes IMatch + 1 and IIMatch 0. IIMatch needs updates for another reason. To revert to the matching position, set IIMatch to 0 during 𝑆-Extension. If the new article matches article qi, set IIMatch to 1 and check if IMatch and IIMatch need revisions after shifting the query sequence. If the extended item 𝑒 is less than qi, the research fails to update IMatch and IIMatch for the 𝐎-Extension sequence. Use the judgment technique to update IIMatch for identical qi or extended item 𝑏. If 𝑏 exceeds qi, set IIMatch to 0. Items are alphabetized in an itemset. Although 𝑽-Extension cannot identify a match for the itemset at position IMatch in the request sequence, the sequence continues. Consider the present sequence <(𝑎), (𝑏)> and the query sequence <(𝑎, 𝑏, 𝑐), (𝑒)>.
To continue 𝐼-Extension, add 𝑐 to the sequence <(𝑎), (𝑏, 𝑐)>. IIMatch and IMatch were adjusted because the expanded item matches the desired item. IIMatch updates automatically if research continues using 𝐎-Extension and item 𝑒. Mismatched location. The explanation is that lists <(𝑎), (𝑏, 𝑐, 𝑒)> and <(𝑎), (𝑏, 𝑐), (𝑒)> vary Former cannot match question a sequence, unlike latter. To fix this, NotUpdate checks IMatch and IIMatch for unupdates. The study won't modify IMatch and IIMatch if NotUpdate is true. By setting NotUpdate to accurate, the growth sequence may run 𝑎-Extension after IMatch modification. After 𝑆-Extension, the NotUpdate argument is set to false. This study will not modify IMatch or IIMatch: IMatch matches the query sequence and matches its size. Start with UTFP, or unpromising transactions filter pruning. NQS transactions are filtered by Database D. Transaction records without qs cannot form sequential patterns.
To save memory and boost efficiency, SPTA deletes irrelevant records for transactions. Mining frequent target sequence patterns is impossible if database D is below minsup before filtering.The study can present the query sequence qs' as a bitmap in [0 0, 0 0 0 1, 0 0 0 0, 0 0 0 1 The research must filter sequences 𝑏1 and 𝑏3 to lower length to [0 0 0 1, 0 0 0 1]. For sequences <(𝑔)> and minsup = 2, support rises to 3 until the uncertain transaction filters pruning method (UTFP) filters them. A maximum support of 1 for the required sequential pattern with 𝑏 leads to more errors. After filtering, Database D contains just 4 entries with the query pattern <(𝑎), (𝑒), (𝑓)>. No frequent target sequence patterns arise if |D| < minsup.Second Method (UPIP, Unpromising Prefix Item Trimming). The bulk of sequential pattern mining algorithms involve recursive growth with shared elements. A study determined the number of sequences with qi after a frequent item 𝑒 through contrasting the bitmaps of 𝑒 and q for a prefix item 𝑒. Researchers write fn. Queries start with qi again. The study does not employ 𝑒 to sustain development when fn is ≤ minsup and qi is absent.
Avoid starting patterns with 𝑏 as there is less support than minsup for any target sequence pattern. There, Study's query sequence qs' = <(𝑎), (𝑏)> has an appropriate minimum value of 2. Since sup(𝑓) = 2 ≥ minsup, it is likely frequent. Comparing UPIP-bitmaps. The query sequence qs' has a qi value of 𝑎 and a bitmap of [0 1 0 0, 1 0 0 0]. Use bitmap [0 0 0 1, 0 0 0 0, 0 0 0 1] for frequent item 𝑓. Of course, UIUP needs zero fn. Stop patterning with the shared object. Indeed, 𝑎 can be used successively, as in <(𝑎), (𝑏), (𝑓)> and sup(<(𝑎), (𝑏), (𝑓)> Plan 3 is the USIP (Disappointing 𝑆-Extension item reduction strategy). The study suggests using USIP to identify sequential patterns for recurrent increase after 𝑆-Extension. After comparing bitmaps, the study identifies sequences where qi follows expanded item 𝑒. Number notation is fn. The study fails to employ 𝑒 as an extended item to improve pattern if fn is below minsup. Thus, using the extended sequential pattern as a prefix is unable to target sequential pattern compatibility above minsup.
The function returns a count of sequences where qi is either equal to or following e if the extended item 𝑒 matches qi. Minsup = 2, currentsequence 𝑦 = <(𝑔)>, and request sequence qs' = <(𝑎), (𝑏)>. Prolonged sequence 𝑠′ = <(𝑏), (𝑏)> is a common pattern, and 𝑆-Extension may expand item 𝑏. Either 𝑎 and qi are important. Bitmaps display 𝑏′ as [0 1 1 0, 0 1 1 0, 0 0 0 0] and qi as [0 1 0 0, 0 1 1 0, 1 0 0 0]. Thus, fn= 1 and 𝑏′ do not apply to the development pattern. The query sequence qs' will have a different sequential pattern if 𝑏′ is extended. For extended item 𝑎, 𝑦′ bitmap is [0 1 0 0, 0 1 1 0, 0 0 0 0]. and fn = 2 ≥ minsup. <(𝑏), (𝑎)> can sustain growth. The desired sequence of query sequences qs' is <<(𝑏), (𝑎), (𝑏)>. Planning 4-UIIP (Unpromising U-Extension item trimming). USIP effectively generates patterns for single-item datasets using 𝑆-Extension. Multiple-element datasets can use 𝐼-Extension, reducing duplicate processes with UIIP. We offer UIIP to identify repeating patterns in 𝐽-Extension.
As in Question 2, we can omit updating IMatch and IIMatch if the expanded item is smaller than qi. If failing, research must rewrite IIMatch and IMatch. Changes in qi and match position. This study must consider two extended item possibilities. At first, qi and 𝑏 are considered equal. Count qi > e sequences with fn. A second case arises when 𝑒 surpasses qi, resulting in IIMatch set to 0. The total amount of sequences with qi greater than e is calculated using fn. The study advises against using item 𝑒 as an extended item when fn is smaller than minsup, wherein qs’ is a query sequence and 𝑒 is a current sequence with minsup = 2. It is clear that 𝐼-Extension can expand 𝑏, 𝑐, and 𝑑. Qi is more significant than 𝑏, which will remain intact. Longer sequence 𝑏′ bitmap is [0 1 0 0, 0 1 0 0], while qi bitmap is [...]. With fn set to 2, the pattern 𝑦′ = <(𝑏), (𝑎, 𝑏)> can go on indefinitely. When item 𝑐 matches, Qi changes to 𝑏. The bitmap of qi is [0 0 1 0, 0 0 1 0]. Prolonged sequence bitmap: [0 1 0 0]. Growth can keep going indefinitely for fn=2 and 𝑏′. If the final item 𝑑 exceeds qi, qi becomes 𝑎. Qi and the expanded sequence 𝑦′ have [0 1 0 0, 0 1 0 0] bitmaps. I shall not use 𝑏′ to create the pattern fn = 1.
b. Proposed SPTA Algorithm
To find patterns in massive datasets, the SPTA algorithm uses a systematic approach. Enter data, filter the database, generate items that appear often, and then prune prefix patterns. Gathering the sequence databases (D), the query sequences (qs’), and the minimum support thresholds are the three inputs needed for the input stage. To speed up mining, the database filtering stage employs the UTFP strategy, which stands for Unpromising Transaction Filter Pruning. In order to construct patterns, the frequent item creation stage produces frequent items. In order to maximize efficiency, the prefix pattern pruning (UPIP) method eliminates unproductive prefix patterns.
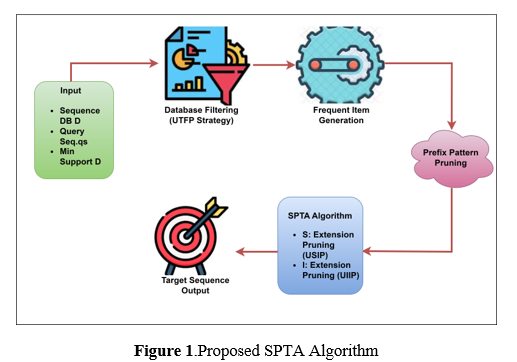
In figure 1 show that the S-extension pruning (USIP) and I-extension pruning (UIIP) techniques are important to the SPTA algorithm and help to enhance performance. Then, patterns are discovered by utilizing the pattern growth with S-extension and I-extension. The outcome is the target sequence patterns that were mined.
Input:
The first step of the process, where the algorithm is fed three parameters: the minimal support threshold, the query sequence (qs’), and the sequence databases (D). Finding patterns in data is the job of the sequence databases. The algorithm's search pattern or sequence in the databases is called the query sequences. A parameter called the minimum support threshold establishes the bare minimum of occurrences required for a pattern to be deemed statistically significant. The pattern mining process cannot begin without these inputs.
UTFP Strategy for Database Filtering:
This section applies UTFP, or Unpromising Transaction Filter Pruning, to the database. This method isolates the transactions that are pertinent to the query sequence by removing all others from the database. This improves the efficiency of the mining process by cutting down on superfluous computation.
Generating Items Regularly:
Scan the filtered database to generate frequent items after filtering the database. What we call "frequent items" are those that show up in the dataset quite often. Finding common items is essential because they provide a foundation for discovering patterns in the collection.
UPIP Strategy for Prefix Pattern Pruning:
This section applies the UPIP (Unpromising Prefix Item Pruning) method. By using this approach, the study wants to weed out prefix patterns that don't have much promise. The technique improves performance by decreasing the amount of needless operations during pattern mining and eliminating unproductive patterns.
SPTA Algorithm:
Several sub-components make up the basic SPTA algorithm, which is represented by this block: S-Extension Pruning (USIP Strategy): In order to enhance performance, this phase entails removing unproductive S-extension items. Things that can be appended to the very end of a sequence are called S-extension items. Here, in order to improve efficiency, unproductive I-extension items are removed. UIIP Strategy: One type of item is the insertion-extension item, which can be used in a sequence. Based on the query sequence and lowest support threshold, the algorithm systematically analyzes the dataset to uncover sequential patterns using S-Extension and I-Extension, a method for pattern growth. It expands patterns by extending them with S-or I-extensions.
Output of the Target Sequence:
This block stands for the algorithm's output step, when the ultimate result is printed out, containing the mined target sequence patterns. These recurring themes indicate significant sequences in the dataset that are a good fit for the query sequence and have enough support to be considered. The SPTA technique is shown in a structured overview by the block diagram, which highlights its main components and the flow of operations from input to output. In this way, we can see how the algorithm effectively finds decided on sequential patterns in massive datasets; each block stands for a different step in the process.
𝑨𝒍𝒈𝒐𝒓𝒊𝒕𝒉𝒎 𝟏: SPTA Algorithm
𝑰𝒏𝒑𝒖𝒕: Sequence database (D).
qs’1: user-provided query sequence; minsup1: user-defined minimum support.
Output: Every targeting sequential patterns of query sequence qs1.
Step 1: filters D sequences without qs (UTFP Strategy)
Step 2: the D is scanned again to identify frequent items (F1),
eliminate infrequent items, construct a bitmap for frequent items, CMAP.
Step 3: Initialize qi is the first items in qs, IMatch is 0, IIMatch is 0;
Step 4: for frequent items <𝑓> in F1 do
initialize fn1 based on the comparison of 𝑓 and qi bitmaps.
if fn1 < minsup1 then
continue (UPIP Strategy)
end
UpdateMatch1(IMatch1, IIMatch1);
Use SEARCH(<𝑓>, F1, {𝑒 ∈ F1 | 𝑒 ≻𝑙𝑒𝑥 𝑓 }, qs1, minsup1, IMatch1, IIMatch1
end
In algorithm 1, Searching a sequence database for sequential patterns that match a user-supplied query sequence and fulfill a user-defined minimum support threshold is made efficient with the Sequential Pattern Targeting Algorithm (SPTA). Several steps make up the algorithm: input, filtering out sequences that do not contain the query sequences, finding common items, setting variables to starting values, iterating over common things, and finally, running the SEARCH process. A user-supplied query sequences (qs1) and a minimum support threshold (minsup) are input into a sequence database (D). To improve efficiency, the UTFP method eliminates sequences that do not include the query sequences. A Conditional Maximum Pattern is formed by identifying frequently used items and creating a bitmap for each of them. The algorithm iteratively processes frequent items using the bitmap of 𝑓 and qi, and variables are initialized for future processing. Using the UPIP technique, the algorithm iterates further if fn1 is below the minimal support level. In response to a user-supplied query sequence, the algorithm returns all target sequential patterns satisfying the minimal support criterion.
𝑨𝒍𝒈𝒐𝒓𝒊𝒕𝒉𝒎 2: Search procedure
𝑰𝒏𝒑𝒖𝒕:
𝑠1: the current sequence;
SE1: a set containing all items can perform 𝑆-Extension;
IE1: a set containing all items can perform 𝐼-Extension;
qs1: a query sequence provided by the user;
minsup1: a minimum support defined by the user;
IMatch1: the matching position of the itemset of the query sequence;
IIMatch1: the matching position of the item in the matching itemset of the query sequence.
1. if IMatch1 == qs1.size1() then
2. output 𝑠1;
3. end
4. initialize 𝑆𝑡𝑒𝑚𝑝 ← ∅, 𝐼𝑡𝑒𝑚𝑝 ← ∅;
5. initialize newIMatch1 ← IMatch1, newIIMatch1 ← IIMatch1;
6. initialize qi ← ∅, 𝑠′ ← <>, fn:=0;
7. for each 𝑓 ∈ SE do
8. if CMAP1(s, 𝑓) < minsup1 then
9. continue;
10. end
11. 𝑠′ = 𝑠 extends 𝑓 by 𝑆-Extension;
12. if sup1(𝑠′) ≥ minsup1 then
13. 𝑆𝑡𝑒𝑚𝑝 = 𝑆𝑡𝑒𝑚𝑝 ∪ 𝑓
14. end
15. end
16. for each 𝑓 ∈ 𝑆𝑡𝑒𝑚𝑝 do
17. 𝑠′ = 𝑠 extend 𝑓 by 𝑆-Extension;
18. newIMatch1, newIIMatch1 = call UpdateMatch1()
19. fn1 = the outcome of associating the bitmaps of 𝑓 with the bitmaps of qi;
20. if fn1< minsup1 then
21. continue;
23. call SEARCH1(𝑠′, 𝑆𝑡𝑒𝑚𝑝, {𝑒 ∈ 𝑆𝑡𝑒𝑚𝑝 | 𝑒 ≻𝑙𝑒𝑥 𝑓 }, qs1, minsup1, newIMatch1, newIIMatch1)
24. end
25. for each 𝑓 ∈ IE do
26. if CMAP1(s, 𝑓) < minsup1 then
27. continue;
28. end
29. 𝑠′ = 𝑠 extends 𝑓 by 𝐼-Extension;
30. if sup(𝑠′) ≥ minsup1 then
31. 𝐼𝑡𝑒𝑚𝑝 = 𝐼𝑡𝑒𝑚𝑝 ∪ 𝑓
32. end
33. end
34. for each 𝑓 ∈ 𝐼𝑡𝑒𝑚𝑝 do
35. 𝑠′ = 𝑠 extend 𝑓 by 𝐼-Extension;
36. newIMatch1, newIIMatch1 = call UpdateMatch1();
37. fn1 = the outcome of associating the bitmaps of 𝑓 with the bitmaps of qi
38. if fn1 < minsup1 then
39. continue;
40. end
41. call SEARCH(𝑠′, 𝑆𝑡𝑒𝑚𝑝, {𝑒 ∈ 𝐼𝑡𝑒𝑚𝑝 | 𝑒 ≻𝑙𝑒𝑥 𝑓 }, qs, minsup, newIMatch, newIIMatch)
42. end
Algorithm 2's Search method is an integral aspect of the SPTA, or Sequential Pattern Targeting Algorithm. It recursively searches for patterns that match the user-provided query sequence (qs’) and fulfill the user-defined minimum support threshold (minsup1), and it also extends the current sequence with new items to investigate sequential patterns inside it. This process requires a number of input parameters, such as the current sequence (𝑦1), items that can execute 𝑆-Extension (SE1), items that can execute 𝐼-Extension (IE1), the user-supplied query sequence (qs1), and the minimum support threshold (minsup1). It is printed out if the size of the current sequence is equal to the corresponding position of the item sets of the query sequences. For every item in the set SE1, the procedure uses the UpdateMatch function to update corresponding positions, initializes variables for subsequent processing, and then repeats the process for items in the set 𝐽-Extension. It also extends the sequence with S-Extension (𝑆-Extension). This optimizes performance by methodically exploring sequential patterns.
5. Experimental Result and Analysis
Using the freely accessible dataset[21] On-Line Retail, a UK-based non-store online retailer, this notebook delves into consumer segmentation. Unique all-occasion gifts are the main focus of the dataset, which includes transactions from 01/12/2010 to 09/12/2011. Primarily, wholesalers are the company's clientele. The term "customer segmentation" refers to the process of identifying distinct groups of customers based on their contacts with a company, most notably their purchasing habits. To better comprehend consumer decision-making processes, market basket analysis is a useful tool for gaining detailed insights into consumer behavior. Customers might not even realize they have biases or patterns in their buying habits, so this is really helpful. The notebook's goal is to provide helpful judgments according to user interests by utilizing association rule mining techniques and unsupervised learning methodologies.
a. Performance Metrics
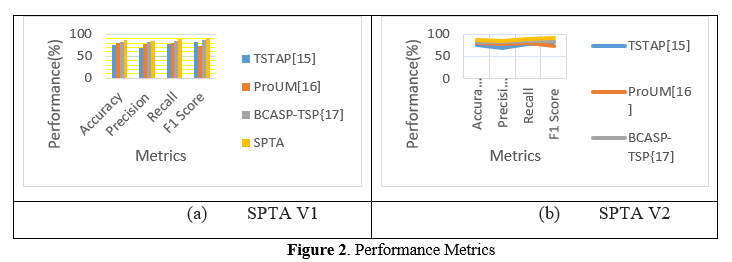
Figure 2(a) and 2(b) shows that relations of accuracy, recall, precision, and F1 score, the Sequential Pattern Targeting Algorithm (SPTA) V1 and V2 performs better than other algorithms. The results that TSTAP, ProUM, BCASP-TSP, and BCASP-TSP achieve are comparable. TSTAP achieves an accuracy of 76%, ProUM achieves an accuracy of 80%, BCASP-TSP achieves an accuracy of 82%, BCASP-TSP achieves an accuracy of 82%, and BCASP-TSP achieves an accuracy of 86%. SPTA surpasses these algorithms in terms of performance metrics, exhibiting greater performance in targeting sequential mining patterns within the dataset. This study is demonstrated within the context of the dataset.
b. Running Time
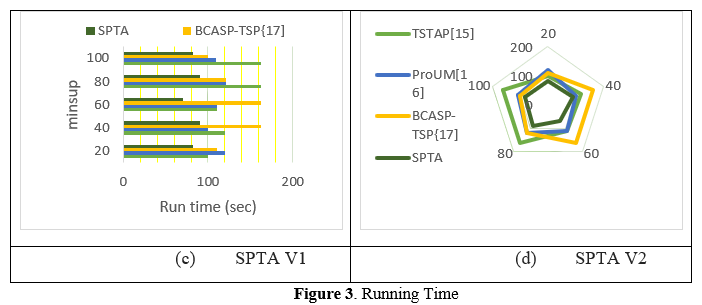
Figure 3(a) and 3(b) showsVarious methods, including TSTAP, ProUM, BCASP-TSP, and SPTA, are compared in terms of their performance indicators under a variety of situations and datasets. The numbers in each column reflect various performance parameters, such as accuracy, precision, recall, or F1 score. Each row corresponds to a distinct dataset or experimental setting, and with each row comes a fresh set of values. An example of this would be the fact that TSTAP achieves a score of 100 in dataset 20, ProUM 120, BCASP-TSP 111, and SPTA 82 for a particular performance criterion. The TSTAP achieves 120, the ProUM reaches 100, the BCASP-TSP earns 162, and the SPTA achieves 91 for the same metric in dataset 40. Utilizing these data, one is able to compare and evaluate the efficiency of these strategies under a variety of circumstances.
c. Scalability
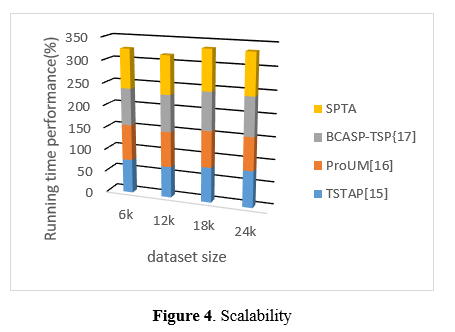
In figure 4,The information presents the performance measurements of TSTAP, ProUM, BCASP-TSP, and SPTA over a variety of dataset sizes. TSTAP achieves an accuracy of 76% for a dataset of 6,000 objects, while ProUM achieves 80%, BCASP-TSP achieves 82%, and SPTA reaches 87%. The accuracy of TSTAP is 70%, whereas that of ProUM is 79%, BCASP-TSP is 82%, and SPTA is 85% when applied to a dataset of 12k. This data offers insights into how each algorithm works across a variety of dataset sizes, enabling comparison and evaluation of the performance of the algorithms under a variety of scenarios. Gaining an understanding of how algorithms scale with the size of the dataset and determining whether any particular method performs better with larger or smaller datasets is facilitated by this.
6. Conclusion and Future work
Improved targeted sequential pattern mining efficiency is the goal of the new Sequential Pattern Targeting Algorithm (SPTA). The CM-SPAM algorithm is used to improve the efficiency of pattern analysis. The study used to large-scale datasets and sequences with many elements, SPTA's performance is optimized by the use of various pruning approaches. Results show that SPTA reduces memory use and achieves faster processing times compared to existing sequential pattern mining (SPM) methods, as tested extensively across datasets. There are certain drawbacks to SPTA, such as the fact that its performance changes according on the features and query sequences of the dataset and that the complexity and diversity of the dataset affect its efficacy. There needs to be additional research and validation in many real-world circumstances since the performance evaluation of SPTA might not account for all potential use cases and datasets. Improving pruning algorithms, incorporating machine learning or predictive analytics, performing extensive validation tests and real-world case studies, and continuously updating and refining SPTA based on user feedback and ongoing pattern mining research are all potential directions for future research focused on addressing these limitations.
References :
[1]. Yang, Aimin, et al. "Review on the application of machine learning algorithms in the sequence data mining of DNA." Frontiers in Bioengineering and Biotechnology 8 (2020): 1032.
[2]. Sundari M, Shanmuga, and Vijaya Chandra Jadala. "SqueezeNet Fusion: Enhancing Rhythmic Heart Disease Classification through Integrated Pattern Mining and Deep Learning." International Journal of Computing and Digital Systems 15.1 (2024): 1-9.
[3]. Gan, Wensheng, et al. "Fast utility mining on sequence data." IEEE transactions on cybernetics 51.2 (2020): 487-500.
[4]. Park, Sangwon, et al. "Spatial structures of tourism destinations: A trajectory data mining approach leveraging mobile big data." Annals of Tourism Research 84 (2020): 102973.
[5]. Fan, Ziwei, et al. "Continuous-time sequential recommendation with temporal graph collaborative transformer." Proceedings of the 30th ACM international conference on information & knowledge management. 2021.
[6]. Wu, Youxi, et al. "ONP-Miner: One-off negative sequential pattern mining." ACM Transactions on Knowledge Discovery from Data 17.3 (2023): 1-24.
[7]. Hu, Kaixia, et al. "Targeted mining of contiguous sequential patterns." Information Sciences 653 (2024): 119791.
[8]. Chen, Zefeng, et al. "TALENT: Targeted mining of non-overlapping sequential patterns." arXiv preprint arXiv:2306.06470 (2023).
[9]. Ezeife, Christie I., and Hemni Karlapalepu. "A Survey of Sequential Pattern Based E-Commerce Recommendation Systems." Algorithms 16.10 (2023): 467.
[10]. Song, Wei, Tin Truong, and Hai Duong. "Pattern Mining: Current Challenges and Opportunities." Database Systems for Advanced Applications. DASFAA 2022 International Workshops: BDMS, BDQM, GDMA, IWBT, MAQTDS, and PMBD, Virtual Event, April 11–14, 2022, Proceedings. Vol. 13248. Springer Nature, 2022.
[11]. Shakeel, Pethuraj Mohamed, Burhanuddin bin Mohd Aboobaider, and Lizawati Binti Salahuddin. "Detecting Lung Cancer Region from CT Image Using Meta-Heuristic Optimized Segmentation Approach." International Journal of Pattern Recognition and Artificial Intelligence 36.16 (2022): 2240001.
[12]. Zhang, Chunkai, et al. "TUSQ: Targeted high-utility sequence querying." IEEE Transactions on Big Data 9.2 (2022): 512-527.
[13]. Sunhare, Priyank, Rameez R. Chowdhary, and Manju K. Chattopadhyay. "Internet of things and data mining: An application oriented survey." Journal of King Saud University-Computer and Information Sciences 34.6 (2022): 3569-3590.
[14]. Leprince, Julien, Clayton Miller, and Wim Zeiler. "Data mining cubes for buildings, a generic framework for multidimensional analytics of building performance data." Energy and Buildings 248 (2021): 111195.
[15]. Zhang, Zhi-Heng, et al. "Tri-partition state alphabet-based sequential pattern for multivariate time series." Cognitive Computation 14.6 (2022): 1881-1899.
[16]. Gan, Wensheng, et al. "ProUM: Projection-based utility mining on sequence data." Information Sciences 513 (2020): 222-240.
[17]. Choong, Shin Siang, et al. "A bee colony optimisation algorithm with a sequential-pattern-mining-based pruning strategy for the travelling salesman problem." International Journal of Bio-Inspired Computation 15.4 (2020): 239-253.
[18]. Court, Robert, et al. "Virtual Fly Brain—An interactive atlas of the Drosophila nervous system." Frontiers in physiology 14 (2023): 1076533.
[19]. Fournier-Viger, Philippe, et al. "Pattern mining: Current challenges and opportunities." International Conference on Database Systems for Advanced Applications. Cham: Springer International Publishing, 2022.
[20]. Miao, Yuantian, et al. "Machine learning–based cyber-attacks targeting on controlled information: A survey." ACM Computing Surveys (CSUR) 54.7 (2021): 1-36.
[21]. https://www.kaggle.com/code/mgmarques/customer-segmentation-and-market-basket-analysis