Efficient Extraction of Patterns in High-Dimensional Data through Tensor Decomposition Techniques

Authors :

Ahmed emjalli and Maisaa Mahasneh

Address :

school of Information science and computing, Donetsk National Technical University, Lviv region, 82111, Ukraine

Department of Information Technology, Al-Huson University College, Al-Balqa Applied University, Jordan

Abstract :

Analyzing big data sets can be difficult due to their intricate patterns and concealed connections.to decrease complexity while retaining essential details necessary for identifying significant trends from this data type. The precision for pattern identification and classification in data with many dimensions, the current study aims to establish a Tensor-Based Pattern Extraction Framework (TPEF). The suggested system employs an organized preparation method to deal with missing values, remove duplication, and standardize the data representation for uniformity. A multi-way tensor can represent the connections among objects. To enable the recognition of noteworthy structures, tensor factorization procedures are used to break down the tensor into lower-dimensional elements. Grouping elements with identical features through methods of clustering improves their comprehension. More exact grouping and data representations are made possible by the test results showing that TPEF increases the effectiveness of sequence extraction. The findings demonstrate that data can be better organized using tensor breakdown, which improves computational effectiveness without losing essential information connections. As an adaptable option for different analytical tasks, the present research shows that tensor-based techniques effectively discover undetected patterns in high-dimensional information.

1.Introduction

Numerous fields in modern information-driven society rely on highly dimensional information, including medical research, the field of economics networking sites, and natural language processing. The advantages and disadvantages of large datasets are proportional to the total amount of measurements, parameters, or characteristics [1]. A pattern retrieval is challenging due to the size and complexity of these historical data, considering the abundance of knowledge that they provide. Applying expensive or missing material conventional statistical techniques to data that is highly dimensional is a real possibility. When working with these types of datasets, pattern identification along with information retrieval require sophisticated techniques that decrease complexity while maintaining complex relationships [2]. Challenges with multidimensional data are investigated in this study using tensor breakdown methods. Computing effort and data simplicity grow dramatically with high-dimensional information due to the enchantment of dimension. Notable methods for reducing dimensionality, such as principal component analysis (PCA) and support vector density (SVD), have been extensively employed to tackle this problem [3]. These approaches fail to grasp the multilinear nature of the information in high dimensions. Efficient pattern extraction from data sets with high dimensions with preserved organisational information as well as reduced redundancies is the problem that the present research aims to tackle. To show that the tensor decomposition method can handle complicated connections while enhancing retrieving information, it is utilised to collections with naming changes.

This study uses tensor decomposition to solve its problem. Tensor decomposition preserves higher-order data dimension interactions better than matrix decomposition. Tensors are its multidimensional arrays [4]. Tucker or CANDECOMP/PARAFAC (CP) tensor decomposition represents the high-dimensional dataset. These methods break down the original tensor into smaller, interpretable parts to reduce dimensionality while preserving structural details. The study's common and original name variants dataset illustrates high-dimensional data's complex relationships. The methodology uses tensor decomposition to simplify data structures, improve retrieval accuracy, and identify patterns [5].

Principal contributions of this research:

• Pattern extraction from high-dimensional data through tensor decomposition. This framework enhances data analysis and decision-making across various domains [6].
• It enhances data retrieval and pattern recognition efficiency and accuracy by maintaining essential structural information and minimizing redundancy. This contribution benefits applications in information management and large-scale data processing.
• The research implements the suggested methodology on a real-world dataset featuring name variations to illustrate its practicality and effectiveness in handling intricate relationships within high-dimensional datasets [7].

The subsequent sections of this paper are structured as follows. Section 2 extensively examines pertinent literature, emphasizing current methodologies for dimensionality reduction and pattern recognition in high-dimensional datasets. Section 3 delineates the comprehensive method, encompassing an exposition of tensor decomposition techniques and their utilization in the dataset. Section 4 presents the experimental results, illustrating the efficacy of the proposed method in identifying significant patterns. Section 5 concludes the study by encapsulating principal findings, delineating contributions, and suggesting avenues for future research.

2. Literature Survey

Mamun et al.[8] This study uses MPCA-based tensor decomposition to extract key features from high-dimensional fabric texture data for real-time fabric weave pattern recognition. High-resolution video recordings segmented into sequential image frames are processed using LBP and GLCM to create the Surface Texture Descriptor Tensor. MPCA reduces tensor dimensionality by 99.99% alongside a minimum of 0.001% information reduction, improving recognition precision over benchmarking approaches. The method improves automatic textile quality control. However, it requires extensive labelled data for trained learning, is sensitive to fabric texture and lighting, and requires substantial computing resources for execution in real-time. Considering these difficulties, the approach suggested boosts industrial material examination productivity and accuracy.

Movahed et al.[9] This research examines tensor decomposition in cancer studies from 2013 to 2023, focussing on highly dimensional imaging and omic data interpretation problems. Tensor breakdown techniques like Tucker and Canonical Polyadic reduction are tested for identifying trends from multivariate cancer information. Tensor techniques improved the accuracy of the extraction and classification of features on freely accessible tumour imaging and genetic resources. Findings show the capacity to reveal physiological knowledge, but the computational difficulty and significant information distortion are drawbacks. The article emphasizes the need for decomposing tensor methods to improve cancer statistical efficiency and accuracy.

Liao et al.[10] The present investigation advances tensor-ring deconstruction with multilayer computing (ConvTR) to reduce excess fitting and rank choosing in sparse data for low-rank tensor completion (LRTC). The data set contains benchmark tensors with incomplete records, and ConvTR uses a multilayer CNN to identify complex relationships. The suggested approach exceeds TR-based and other network-based completeness models about reconstructed data precision and durability. Due to multilayer activities, the amount of computing required is high, and performance depends on information sparseness and organization. Though limited, ConvTR improves tensor conclusion, rendering it appropriate for complicated information restoration workloads.

Chen et al.[11] The Tensor Linear Discriminant Analysis with Missing Data (Tensor LDA-MD) algorithm for classifying high-dimensional tensors with incomplete observations under the MCR assumption is introduced in this study. The method models class dependencies using the Tensor Gaussian Mixture Model (TGMM) and estimates the discriminant tensor using low-rank decomposition. Its resilience is shown by its excellent precision in classification regardless of large values absent in artificial and real-world databases, encompassing health imaging and hyperspectral images. Tensor LDA-MD improves conventional approaches, but the computational expense and order decision susceptibility limit it. This research lays the groundwork for further developing tensor-based categorization with data shortages.

Sandoval et al.[12]This study presents an integer decomposition-based supervised data analysis method for multidimensional intelligent meters data, especially Electricity Consumption Profiles. Data is structured as a three-way tensor, simplifying information compression, visualization, and classification while iteratively managing missing values. The structure is validated using ERCOT data, showing it can gather more information than matrix-based approaches. Identifying patterns and detecting anomalies in energy use enhanced, but computation effectiveness and adaptability for massive data sets remained issues.

Maruhashi et al.[13] This study introduces MultiAspectForensics, a scalable tensor analysis algorithm for heterogeneous network subgraph pattern detection and visualization. The proposed method finds dense bipartite structures with shared attributes for social network analysis and cybersecurity monitoring. The technique extracts hidden interaction patterns from web knowledge bases, network traffic, and social networks by capturing network data's spectral properties. Experimental results show it can detect anomalous behaviours like port-scanning. The algorithm excels at pattern discovery and scalability, but handling high-dimensional data and optimizing computational efficiency for real-time applications is challenging.

3. Proposed Methodology

a) Tensor-Based Pattern Extraction Framework (TPEF) Overview

The illustration depicts a tensor breakdown methodology employed for analyzing information. Raw data is first collected and transformed into an organized tensor format. The procedure involves populating tensor elements and managing dense presentations. The tensor, depicted as a rectangular object with dimensions such as time and nodes, is decomposed by removing significant variables. The decomposition produces three essential components: time factor and two instances of node factor. The extracted factors are subsequently visualized using score graphs, illustrating variations and trends in the data. This method facilitates pattern recognition and anomaly detection in datasets, including network traffic, social interactions, and time-series data.

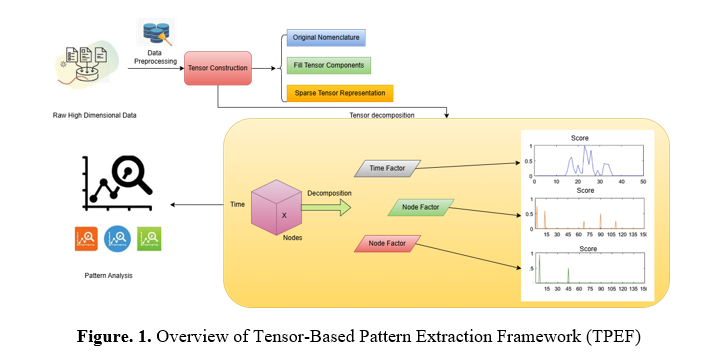
b) Data Preprocessing

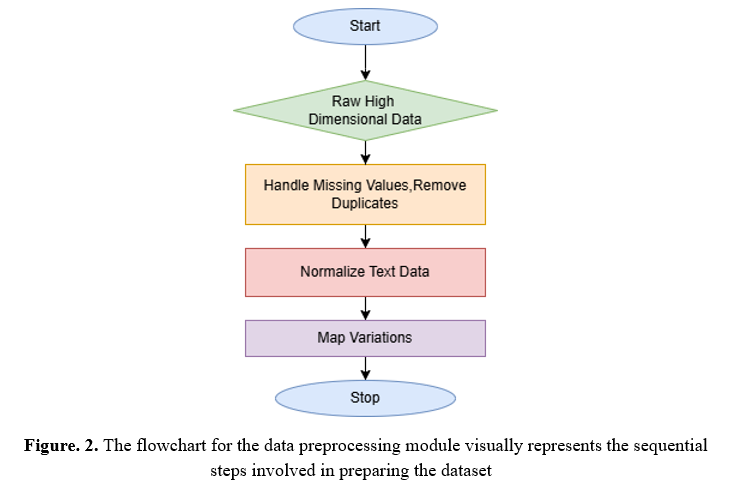
Inconsistencies, absent data, and redundancy in high-dimensional datasets can impede data analysis. Before employing tensor decomposition techniques, these datasets must undergo efficient preprocessing. Data preprocessing sanitizes, normalizes, and readies data for precise tensor transformation, maintaining structural integrity while eliminating noise and redundancy.

Step1:Preliminary Data Sanitisation The initial preprocessing phase involves rectifying absent values, eliminating redundant entries, and addressing dataset inconsistencies. Incomplete fields in datasets are prevalent in high-dimensional data. The absence of data can distort the analysis. Absent or null records are removed or imputed by the dataset's context. Duplicates can skew pattern recognition outcomes and are detected and eliminated to guarantee dataset uniqueness. Rectifying inconsistencies, particularly in name variations or entity formats, is crucial for data cleansing. The dataset distinguishes between "Keith, Adam E" and "Adam Keith," despite referring to the same individual. Rectifying discrepancies guarantees consistency and enhances analysis.

Step 2: Data sanitization precedes normalization. Standardizing data via normalization diminishes variability resulting from inconsistent data representation. Converting all text to lowercase facilitates case-insensitive comparisons. Eliminate special characters, extraneous spaces, and irrelevant punctuation marks that do not contribute to pattern extraction and may introduce noise into the dataset. These normalization methods structure and standardize the dataset, ensuring consistent entity representation across records.

Step 3: Mapping Variations is an identical entity that may be recorded in various formats within high-dimensional datasets. Dataset managers frequently encounter this issue with names or other textual attributes. Data preprocessing proceeds with the standardization of variations of the same entity. Consequently, tensor construction and decomposition manage all references to the identical entity uniformly. The names "bin Abd al-Aziz Al Saud, Abdullah" and "Abdullah bin Abd al-Aziz Al Saud" are consolidated. This mapping step enhances extracted patterns by preventing entity fragmentation caused by inconsistent naming.

c) Tensor Construction

The sanitized information must be utilized to build an organized multi-way tensor during data processing. Tensors allow organized representations of multiple communication and multi-relational information by generalizing matrices (1D) and combinations (2D) to higher-dimensional environments. Multidimensional statistics require transforming them to capture intricate connections. The generated tensor is used for tensor breakdown, which factorizes it to produce lower-dimensional elements. The resulting structure simplifies information while retaining significant trends for effective data extraction and reduced dimensionality. Data hidden patterns and interactions are separated using tensor reduction methods like Canonical Polyadic (CP) and Tucker.

A multi-way tensor τ of order N is expressed mathematically as:

Here, I_n Denotes the number of dimensions of mode n. Tensor components are identified using several dimensions to capture multidimensional connections. By constructing the information set as a tensor, researchers prepare it for deconstruction techniques that identify variables, structures, and groupings. This phase is essential for sophisticated artificial designs and information mining programs, and based on artificial intelligence forecasting, it provides tensor-based interpretations as an effective instrument for intricate data sets.

The steps in Tensor Construction are:

Step 1: Define Dimensions (Modes): Determine essential characteristics to denote as tensor dimensions.

Step 2: Original Nomenclature: Variants of names in the unprocessed data. Common Names: Standardized variants following preprocessing. Categories: Metadata or affiliations about the names.

Step 3: Populate Tensor elements: Every sanitised information item represents interactions across variables. Navigate the information set, linking items to their respective tensor indexes. Populate tensors at these indexes to signify interactions.

Step 4: Employ Minimal Tensor Depiction: Implement a sparse structure to handle huge databases by retaining only non-zero components and their associated indexes. Reduces the use of memory and enhances tensor computations.

A well-structured tensor embodies connections throughout information and enables effective evaluation via deconstruction techniques. Sparse encoding enhances adaptability for huge data sets.

d) Tensor Decomposition

This module seeks to diminish the number of dimensions of a multi-way tensor and identify significant trends. Tensor reduction streamlines presentation without preserving important details by uncovering hidden patterns and associations within the information being presented. Key Tensor Decomposition Techniques CANDECOMP/PARAFAC for CP Decomposition:

One effective method for reducing complex information to more manageable and interpretable chunks is tensor compression. By taking the outermost combination of the matrices from every possible mode, this technique reduces an integer to its rank-one elements. Decreasing the amount of information and identifying significant trends are both aided by this analysis. Alternating Least Squares (ALS) is a popular optimisation method that can improve this entire procedure. ALS fixes a few variables matrices and modifies the remaining ones in a continuous process to reduce the tensor's mistake in reconstruction. To make sure the decomposing variables are good representations of the initial information organisation, this iterative improvement keeps going through completion.

Decomposing a Tucker System:

• Tucker's decompose minimises the dimension to an inferior core component through combining it with factors multipliers for every phase.
• The fundamental tensor records component-to-component interactions in all options, while the factorisation matrix show interconnections in every mode.
• The degree of complexity and precision of a representation are determined by the rank of the component parts, which is also known as rank choosing. Choosing the right rank is crucial for achieving an appropriate balance between comprehensibility and computational effectiveness.
• Tucker decomposed allows for more flexible representation of the tensor between phases when their order of magnitude are distinct.

Two parameters are required to specify the desired decomposition number: the multi-way tensor (T) and the rank (R). Matrix initialization: The matrices A, B, and C are initially set to a random value. The third matrix is updated by solving a least-squares problem during each iteration, while two matrices are fixed. This process continues until the reconstruction errors converge when no more changes occur. The factor matrices (A, B, C) represent the decomposed tensor components as output.

e) Pattern Extraction and Analysis

Multidisciplinary tensor constituent reduction reveals information trends, relationships, and hierarchies. This method converts a multidimensional tensor through constituent matrix structures describing its modes. These architecture matrices capture information's intricate connections among instances and constituents. Analyzing the mentioned factor combinations' organization reveals interesting and pertinent relationships. The matrix entries are extremely valuable in that they often indicate profound connections between individuals alongside particular elements, demonstrating connections between information or interactions.

These highly valuable keywords help aggregate entities that are comparable. Similar designs across components in factors matrices sections or rows indicate relatedness or clustering. In an information set analyzing the behaviour of consumers, individuals with highly valuable items in common elements might possess identical demographics, purchasing patterns, or inclinations.

Those component multipliers may be subsequently clustered using k-means or ascending clustering to recognize and categorize individuals with comparable tendencies. The original material hides organic patterns and connections, but these categories display them. This method helps investigators and analysts draw practical inferences and make decisions based on transparent information.

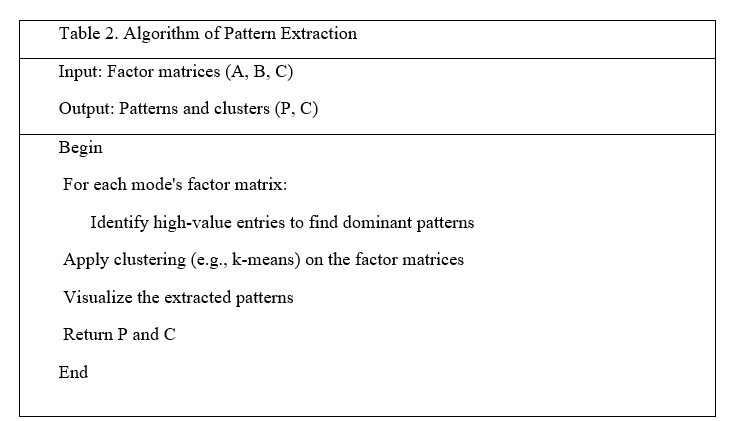
Factor matrices can be clustered using k-means. Clustering entities by shared characteristics across decomposed components helps us find groups with similar behaviour or attributes. This step improves customer segmentation, topic modelling, and extensive dataset entity categorization.

4. Experimental Analysis

a) Reconstruction Error (RMSE)

RMSE evaluates how well the deconstructed tensor recreates the information in the file. The median square variance of the initially generated tensor quantities and the factorized numbers are calculated. A smaller RMSE suggests faster segmentation and less data loss. For tensor factorization ranking decisions, preserving significant connections with minimal distortion in recovered structures is crucial. RMSE is employed in the compression of information, modelling for prediction, and processing of signals to maintain information consistency.

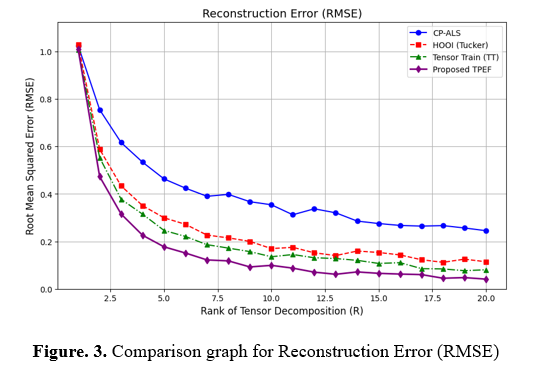
The information set has two essential characteristics, Original Name and Common Name, corresponding to entities' basic and standardized identities. A multi-way tensor is created to analyze relationships and patterns in this information using name rule variants. CP-ALS, Tucker, and Tensor Train (TT) Compression may obtain significant information from these hierarchical representations. Factorizing a tensor through lower-dimensional elements reveals concealed relationships and clustering of similar entities, improving naming confusion, topic conclusion, and recognition of patterns. The most compelling data structure-preserving reduction approach is determined by assessing the reconstruction error (RMSE) across ranks. This approach improves data preprocessing, NLP, and information discovery, providing greater precision in connections among entities in massive databases.

b) Clustering Accuracy (ARI)

A Modified Rand Index measures how effectively recovered component matrix cluster entities that are comparable relative to underlying reality clustering. It accounts for a variance to ensure statistically noteworthy grouping findings. Greater ARI levels (closer to 1) demonstrate that groups precisely represent information structures, while numbers near 0 imply arbitrary allocations. ARI identifies learners with comparable intellectual characteristics who use adaptive educational methods to personalize education. This measurement technique is used in computational biology, analysis of social networks, and recommendation systems to find concealed trends.

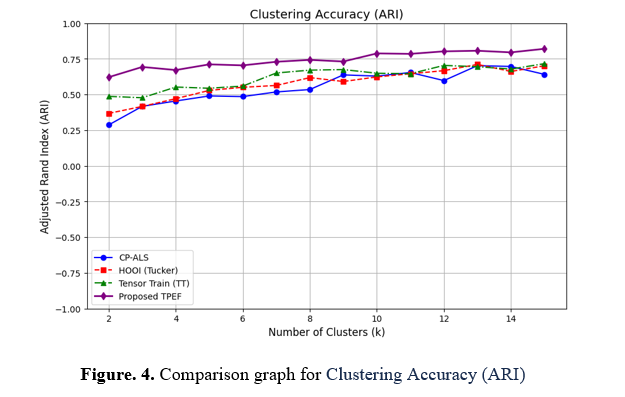
This program plots Clustering Accuracy (ARI) vs. Number of Clusters (k) for CP-ALS, Tucker (HOOI), Tensor Train (TT), and the recommended TPEF algorithm. A collection of Original Names and Common Name combinations is used for classification. They are linked by mapping each original name to its common name. How every algorithm clusters comparable names, the program replicates clustering accuracy (ARI) for numbers ranging from 2 to a customized maximum k_max. The ARI numbers of the dataset's tensor interpretations are used to evaluate segmentation effectiveness, and more significant ARI numbers suggest more excellent grouping. The application utilizes simulated information for ARI and produces a horizontal plot that illustrates the statistical efficacy of every tensor-splitting method in gathering comparable names and recognizing similarities in the analyzed data.

c) Model Complexity (Computational Time & Memory Usage)

This indicator measures processing memory and time usage to evaluate the decomposed tensor efficiency. Flexibility and rapid processing are achieved by optimizing the complexity of models for enormous tensors. Tensor-based neural networks are better for large datasets due to faster convergence and reduced memory consumption. Effective decomposing tensors enable personalized educational institutions to update learning pathways quickly and make actual time-adaptable suggestions according to individuals' Intelligence tendencies. This measure maintains precision, rapidity, and utilization of resources in massive applications.

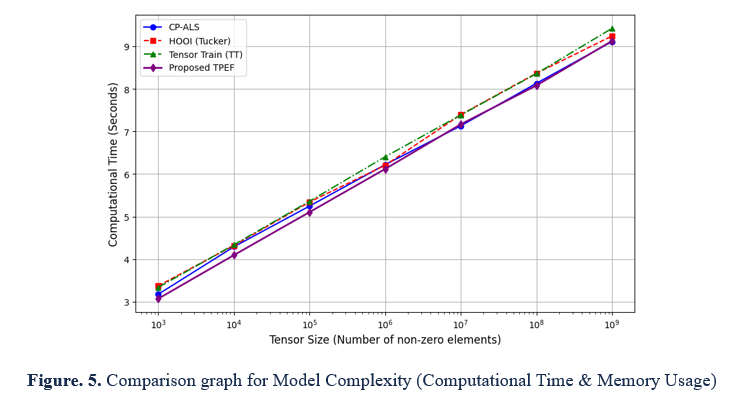
The application generates a chart that contrasts the computational time for CP-ALS, Higher-Order Orthogonal Iteration (HOOI), Tensor Train (TT) Decomposition, and the Proposed Tensor-Based Pattern Extraction Framework (TPEF) depending on the tensor dimensions. The database contains pairs that include the initial and common names, such as "111th Congress" transferred to "111th Congress" and "bin Abd al-Aziz Al Saud, Abdullah" translated to "Abdullah bin Abd al-Aziz Al Saud," indicating connections among entities. The following program demonstrates how every deconstruction technique manages growing tensor dimensions (exponentially spaced from 10^3 to 10^9). Tensor size (greater than zero components) is displayed on the x-axis, while the computational duration (in seconds) is on the y-axis. The line graph shows how well each approach expands with information dimension, comparing massive amounts of Decomposition of Tensors performances.

5. Conclusion and Future Work

The suggested Tensor-Based Pattern Extraction Framework (TPEF) achieves efficient pattern recognition and categorization to simplify complex information while maintaining essential connections. Despite sacrificing critical relationships, findings show that decomposing tensors increases computational effectiveness and enhances information organization. The design improves the understanding of retrieved patterns by incorporating clustering methods, making it an invaluable instrument for many analysis applications. Improving the structure in future versions can include adding support for volatile datasets that necessitate ongoing tensor factorization for real-time updates. Advanced optimization techniques can be integrated to decrease computational difficulty further and improve scalability. Combining deep learning algorithms with tensor-based methodologies could enhance pattern identification and automatic decision-making in significant data settings.

References :

[1]. Petrović, A., & Milošević, J. (2021). Tensor Decompositions for Large-Scale Data Mining: Methods for Uncovering Latent Patterns in Multidimensional Big Data. Journal of Big-Data Analytics and Cloud Computing, 6(2), 12-22.

[2]. Gao, Y., Zhang, G., Zhang, C., Wang, J., Yang, L. T., & Zhao, Y. (2021). Federated tensor decomposition-based feature extraction approach for industrial IoT. IEEE Transactions on Industrial Informatics, 17(12), 8541-8549.

[3]. Xia, Z., Chen, Y., & Xu, C. (2021). Multiview PCA: A feature extraction and dimension reduction methodology for high-order data. IEEE Transactions on Cybernetics, 52(10), 11068-11080.

[4]. Deng, Y., Tang, X., & Qu, A. (2023). Correlation tensor decomposition and its application in spatial imaging data. Journal of the American Statistical Association, 118(541), 440-456.

[5]. Han, Z. L., Huang, T. Z., Zhao, X. L., Zhang, H., & Liu, Y. Y. (2023). Multidimensional data recovery via feature-based fully-connected tensor network decomposition. IEEE transactions on big data.

[6]. Duan, L., Yang, L., & Guo, Y. (2025). Paramps: Convolutional neural networks based on tensor decomposition for heart sound signal analysis and cardiovascular disease diagnosis. Signal Processing, 227, 109716.

[7]. Al-Sarayrah, Ali. "RECENT ADVANCES AND APPLICATIONS OF APRIORI ALGORITHM IN EXPLORING INSIGHTS FROM HEALTHCARE DATA PATTERNS." PatternIQ Mining.2024, (1)2, 27-39. https://doi.org/10.70023/piqm24123

[8]. Mamun, A. A., Islam, M. I., Shohag, M. A. S., Al-Kouz, W., & Noor, K. M. Multilinear Principal Component Analysis-Based Tensor Decomposition for Real-Time Fabric Weave Pattern Recognition from High-Dimensional Streaming Data. Multilinear Principal Component Analysis-Based Tensor Decomposition for Real-Time Fabric Weave Pattern Recognition from High-Dimensional Streaming Data.

[9]. Movahed, E. A., Koleini, F., & Tabrizi, N. (2024). Tensor decompositions in cancer study; A comprehensive. In Proceedings of 36th International Conference on (Vol. 97, pp. 101-113).

[10]. Liao, T., Yang, J., Chen, C., & Zheng, Z. (2024). A neural tensor decomposition model for high-order sparse data recovery. Information Sciences, 658, 120024.

[11]. Chen, E., Han, Y., & Li, J. (2024). High-dimensional tensor discriminant analysis with incomplete tensors. arXiv preprint arXiv:2410.14783.

[12]. Sandoval, B., Barocio, E., Korba, P., & Sevilla, F. R. S. (2020). Three-way unsupervised data mining for power system applications based on tensor decomposition. Electric Power Systems Research, 187, 106431.

[13]. Maruhashi, K., Guo, F., & Faloutsos, C. (2011, July). Multiaspectforensics: Pattern mining on large-scale heterogeneous networks with tensor analysis. In 2011 international conference on advances in social networks analysis and mining (pp. 203-210). IEEE.